现实世界的数据可能多种多样,有的离散,有的连续,有的取值非负,还有的可能有定和效应。货币交易数据,原则上有最小的货币单位所以就可以离散。温度压力等的测量数据,可能就得当作连续数据。商铺客流量数据,其本身应该就是取值非负。地球化学中某一种矿物内元素成分比例总和固定为100%,这样各个成分家在一起就有定和,因此而互相影响,这就是定和效应。
数据繁杂多样,而很多经典的数学和数据科学当中的方法原本可能是针对实数设计的,或者有的概率领域的方法或者模型是针对0均值设计的,因此难以直接应用。面对这种情况,在数据科学与深度学习的实践中,标准化(Standardization)或归一化(Normalization)就是预处理阶段不可或缺的一环。其核心目标在于消除不同特征之间的量纲差异,使模型训练更稳定、收敛更快、结果更具可比性。
然而,并非所有“标准化”方法都遵循相同逻辑;它们在计算步骤、所需统计量、对异常值的敏感性以及适用场景上存在显著差异。以下将系统梳理几种主流方法,明确其操作流程、依赖变量,并简单地对比一下。
一、Z-score 标准化(StandardScaler)
Z-score 是最经典的标准化方法,适用于近似正态分布的数据。其操作分为三个明确步骤:
-
计算均值:对某一特征的所有样本值 $x_1, x_2, \dots, x_n$,计算其算术平均: $$ \mu = \frac{1}{n} \sum_{i=1}^{n} x_i $$
-
计算标准差: $$ \sigma = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2 } $$ (注:在样本估计中常使用 $n-1$ 作分母,但在机器学习预处理中通常用 $n$)
-
逐点变换: $$ z_i = \frac{x_i - \mu}{\sigma} $$
此方法引入两个额外变量:$\mu$ 与 $\sigma$。优点是使数据均值为 0、标准差为 1,适合大多数线性模型;缺点是对异常值敏感,因均值和方差易被极端值扭曲。
二、Min-Max 归一化(MinMaxScaler)
该方法将数据线性压缩至固定区间(通常为 $[0, 1]$),适用于已知边界且无严重异常值的情形。其步骤如下:
-
确定极值:找出该特征的最小值 $x_{\min}$ 与最大值 $x_{\max}$。
-
计算极差:$R = x_{\max} - x_{\min}$。
-
逐点变换: $$ x'i = \frac{x_i - x $$}}{R
仅需两个额外变量:$x_{\min}$ 与 $x_{\max}$。优点是保留原始比例关系,输出直观;缺点是若新数据超出原极值范围,将导致 $x' < 0$ 或 $x' > 1$,且对异常值极为敏感。
三、RobustScaler(稳健标准化)
为应对异常值问题,RobustScaler 使用中位数与四分位距(IQR)替代均值与标准差:
-
计算中位数:$Q_2 = \text{Median}(x)$。
-
计算第一与第三四分位数:$Q_1$ 与 $Q_3$,进而得 IQR: $$ \text{IQR} = Q_3 - Q_1 $$
-
逐点变换: $$ x'_i = \frac{x_i - Q_2}{\text{IQR}} $$
需三个额外变量:$Q_1, Q_2, Q_3$。因其基于分位数,对异常值鲁棒性强,但计算成本略高,且不保证输出范围。
四、MaxAbs 标准化
专为稀疏数据设计,不改变零值结构:
-
计算绝对值最大值:$M = \max(|x_i|)$。
-
逐点变换: $$ x'_i = \frac{x_i}{M} $$
仅需一个额外变量 $M$。输出范围为 $[-1, 1]$,适用于文本向量等稀疏矩阵,但同样对异常值敏感。
五、Layer Normalization(层归一化)
在深度学习中,LayerNorm 对单个样本的所有特征维度进行标准化,常用于 Transformer 等 NLP 模型。其步骤如下:
-
对单个样本 $x = (x_1, \dots, x_d)$,计算其均值与标准差: $$ \mu = \frac{1}{d} \sum_{j=1}^{d} x_j, \quad \sigma = \sqrt{ \frac{1}{d} \sum_{j=1}^{d} (x_j - \mu)^2 } $$
-
标准化: $$ \hat{x}_j = \frac{x_j - \mu}{\sqrt{\sigma^2 + \epsilon}} $$
-
可学习缩放与平移(affine 变换): $$ y_j = \gamma \hat{x}_j + \beta $$ 其中 $\gamma$ 与 $\beta$ 为可训练参数,初始通常设为 1 和 0。
LayerNorm 引入两个统计量($\mu, \sigma$)及两个可学习参数。其优势在于不依赖 batch size,适合变长序列;但需计算均值,可能受极端特征值影响。
六、RMSNorm(均方根归一化)
RMSNorm 是 LayerNorm 的简化变体,近年在 Llama 等大模型中广受青睐。其关键区别在于跳过均值计算:
-
对单个样本 $x = (x_1, \dots, x_d)$,直接计算均方根(RMS): $$ \text{RMS}(x) = \sqrt{ \frac{1}{d} \sum_{j=1}^{d} x_j^2 } $$
-
归一化: $$ \hat{x}j = \frac{x_j}{\sqrt{ \text{RMS}(x)^2 + \epsilon }} = \frac{x_j}{\sqrt{ \frac{1}{d} \sum $$}^{d} x_k^2 + \epsilon }
-
可选缩放(通常保留 $\gamma$,省略 $\beta$): $$ y_j = \gamma \hat{x}_j $$
RMSNorm 仅需一个统计量(RMS)和一个可学习参数($\gamma$)。由于不减均值,计算更高效,且对特征间的偏移不敏感,更适合大模型训练。但其无法消除特征整体偏移,在某些任务中可能不如 LayerNorm 精细。
七、Logarithmic Centering(对数中心化)
对数中心化是一种专门处理右偏分布(如收入、点击率、计数数据)的标准化方法,特别适用于具有定和效应的数据。其核心思想是通过对数变换压缩数据尺度,再进行中心化。
-
对数变换(通常使用自然对数): $$ z_i = \ln(x_i + 1) $$ (加1是为了处理零值)
-
计算对数均值: $$ \mu_z = \frac{1}{n} \sum_{i=1}^{n} z_i $$
-
中心化: $$ z'_i = z_i - \mu_z = \ln(x_i + 1) - \mu_z $$
需两个额外变量:$\mu_z$(对数均值)和变换后的值 $z_i$。优点是能有效处理长尾分布,减轻极端值影响,特别适合处理具有定和约束的比例数据;缺点是要求数据非负,且对零值需要特殊处理。
应用场景: - 生物信息学中的基因表达数据 - 推荐系统中的用户行为计数 - 地球化学中具有定和效应的成分比例数据
八、CLR (Centered Log-Ratio) Transform(中心对数比变换)
CLR变换是专门为定和数据(compositional data)设计的标准化方法,如地球化学中的矿物成分、微生物群落的相对丰度等。这类数据的特点是各成分之和恒定(如100%),因此成分间存在负相关关系。
-
几何均值计算: $$ G(x) = \left( \prod_{i=1}^{D} x_i \right)^{1/D} $$ 其中 $D$ 为成分维度数。
-
CLR变换: $$ \text{clr}(x)_i = \ln\left( \frac{x_i}{G(x)} \right) $$
-
性质:变换后满足 $\sum_{i=1}^{D} \text{clr}(x)_i = 0$。
CLR引入一个几何均值变量 $G(x)$。其优势是能消除定和约束带来的虚假相关性,使成分间关系更真实;但变换后数据维度不变,仍处于 $D-1$ 维的单纯形空间。
注意:CLR变换要求所有成分值严格大于0。
九、ISOMAP标准化(等距映射标准化)
这是一种基于流形学习的非线性标准化方法,适用于数据分布在低维流形上的情况:
-
构建邻域图:根据距离阈值或K近邻构建数据点间的连接关系。
-
计算测地距离:使用Dijkstra或Floyd算法计算流形上的最短路径距离。
-
多维缩放(MDS):将测地距离矩阵映射到低维欧氏空间。
-
标准化:对降维后的坐标进行Z-score标准化。
该方法无需显式统计量,但计算复杂度较高 $O(n^2 \log n)$。适用于高维非线性数据的预处理。
十、Quantile Transformation(分位数变换)
将任意分布的数据映射为指定的目标分布(通常是均匀分布或正态分布):
-
经验累积分布函数(ECDF): $$ F_n(x) = \frac{1}{n} \sum_{i=1}^{n} \mathbb{I}(x_i \leq x) $$
-
分位数映射: $$ x'_i = G^{-1}(F_n(x_i)) $$ 其中 $G^{-1}$ 为目标分布的逆累积分布函数。
当目标分布为正态分布时,也称为分位数归一化(Quantile Normalization)。该方法完全消除原始分布形状的影响,但会丢失数据的局部结构信息。
十一、Unit Vector Scaling(单位向量缩放)
将每个样本向量缩放为单位长度,常用于文本和推荐系统:
$$ x'i = \frac{x_i}{|x|_2} = \frac{x_i}{\sqrt{\sum $$}^{d} x_j^2}
仅需计算向量的L2范数。保持向量方向不变,输出范围为超球面。适用于余弦相似度计算。
十二、Decimal Scaling(小数定标标准化)
通过移动小数点位置进行标准化:
-
确定缩放因子:找到使得 $\max(|x_i|) < 1$ 的最小整数 $j$: $$ j = \lceil \log_{10}(\max(|x_i|)) \rceil $$
-
变换: $$ x'_i = \frac{x_i}{10^j} $$
该方法简单直观,适用于数据范围跨度较大的情形。
方法对比总结表
| 方法 | 额外统计量数量 | 所需变量 | 是否依赖 Batch | 对异常值敏感 | 是否可学习参数 | 典型应用场景 |
|---|---|---|---|---|---|---|
| Z-score | 2 | $\mu, \sigma$ | 否 | 是 | 否 | 线性模型、SVM、PCA |
| Min-Max | 2 | $x_{\min}, x_{\max}$ | 否 | 极强 | 否 | 神经网络输入、图像像素 |
| RobustScaler | 3 | $Q_1, Q_2, Q_3$ | 否 | 否 | 否 | 含异常值的表格数据 |
| MaxAbs | 1 | $\max(|x|)$ | 否 | 是 | 否 | 稀疏数据(如 TF-IDF) |
| LayerNorm | 2 | $\mu, \sigma$(每样本) | 否 | 中等 | 是($\gamma, \beta$) | Transformer、NLP 模型 |
| RMSNorm | 1 | $\text{RMS}(x)$(每样本) | 否 | 较低 | 是(通常仅 $\gamma$) | 大语言模型(如 Llama) |
| Log-Centering | 1 | $\mu_{\ln}$(对数均值) | 否 | 较低 | 否 | 右偏分布、计数数据、定和数据 |
| CLR Transform | 1 | $G(x)$(几何均值) | 否 | 中等 | 否 | 定和数据(成分分析) |
| ISOMAP Norm | 0 | 邻域图、距离矩阵 | 否 | 低 | 否 | 流形数据、高维非线性数据 |
| Quantile Trans | 1 | ECDF 或目标分布 | 否 | 极低 | 否 | 分布形状校正、批次效应校正 |
| Unit Vector | 1 | $|x|_2$(L2范数) | 否 | 中等 | 否 | 文本向量、推荐系统 |
| Decimal Scaling | 1 | 缩放因子 $10^j$ | 否 | 中等 | 否 | 大范围数值数据 |
标准化方法的选择应基于数据分布特性、是否存在异常值、模型架构需求以及计算效率考量。
- 传统机器学习:多采用 Z-score 或 Min-Max
- 现代深度学习:倾向于 LayerNorm 或其高效变体 RMSNorm
- 定和效应数据:必须使用 CLR 变换
- 右偏分布数据:推荐 Log-Centering
- 高维流形数据:可考虑 ISOMAP 标准化
- 批次效应校正:Quantile Transformation 效果显著
理解每种方法背后的计算步骤与变量依赖,方能在复杂建模任务中做出精准而优雅的技术决策。选择合适的标准化方法对于避免虚假相关性和获得可靠模型结果至关重要。
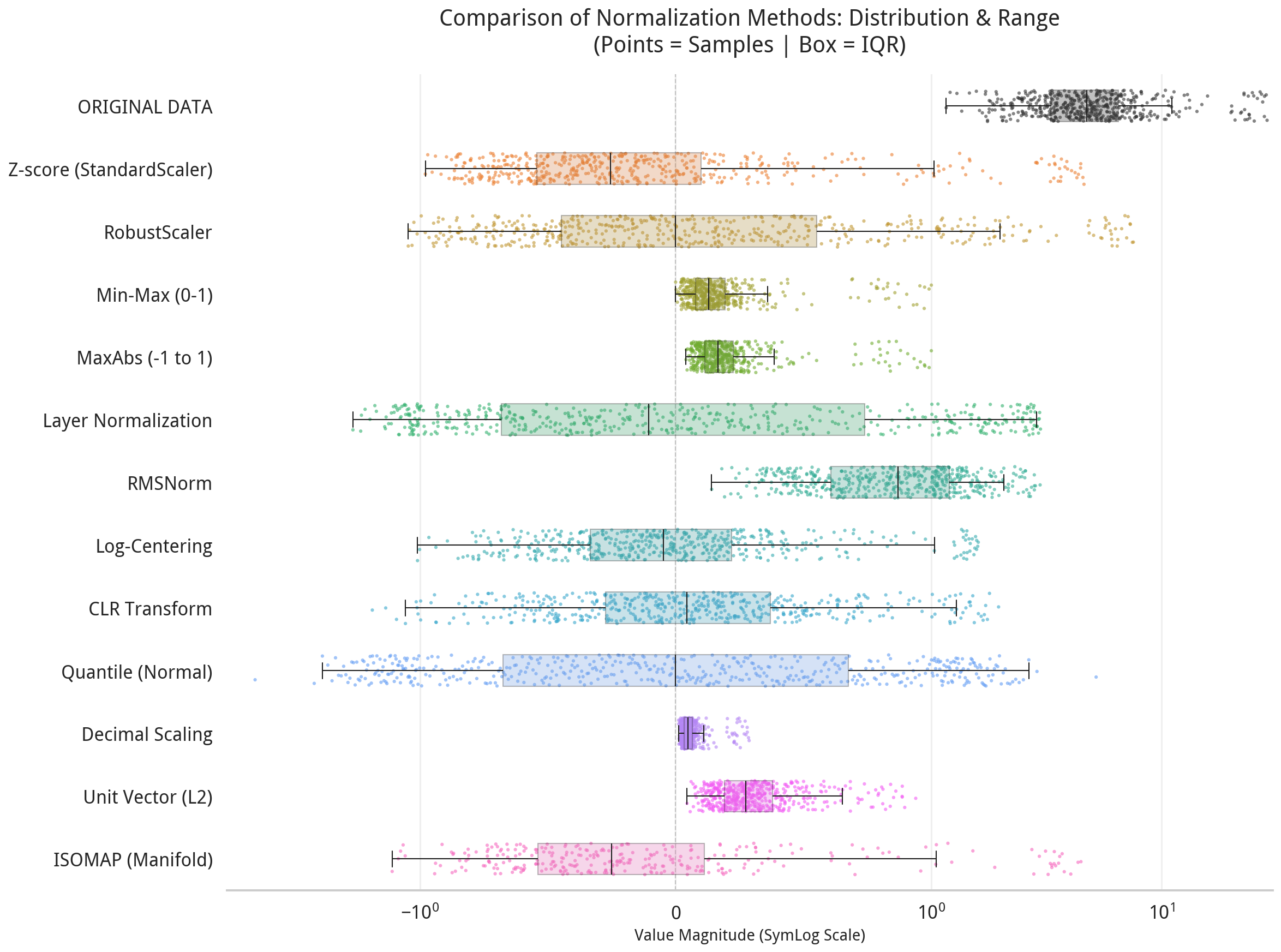
下面的的Python代码对上面提到的各个方法做了简单的可视化对比:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler, MaxAbsScaler, QuantileTransformer, Normalizer
from sklearn.manifold import Isomap
import warnings
import pandas as pd
import platform
# Suppress warnings
warnings.filterwarnings('ignore')
# Set aesthetic style
sns.set(style="whitegrid", context="talk")
# Configure fonts for Chinese support and correct minus sign
system = platform.system()
if system == 'Windows':
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimHei', 'Arial']
elif system == 'Darwin':
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'PingFang SC']
else:
plt.rcParams['font.sans-serif'] = ['WenQuanYi Micro Hei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False # Use ASCII hyphen for minus sign
def generate_visible_data(n_samples=500, n_features=10):
"""
Generate data that is 'badly behaved' (skewed, outliers)
but within a reasonable range (0-30) to be comparable with normalized data (-3 to 3).
"""
np.random.seed(42)
# 1. Base: Log-Normal centered around 5.0 (approx)
# Mean = exp(mu + sigma^2/2)
# If we want mean ~5, let's use mu=1.5, sigma=0.5 -> exp(1.5+0.125) ~ 5.0
data = np.random.lognormal(mean=1.5, sigma=0.5, size=(n_samples, n_features))
# 2. Add moderate outliers (e.g., values around 25-30)
# Not too extreme so they fit on the plot
n_outliers = int(0.05 * n_samples)
outlier_indices = np.random.choice(n_samples, n_outliers, replace=False)
data[outlier_indices, 0] = np.random.uniform(20, 30, size=n_outliers)
# Ensure strictly positive for Log methods
data = np.maximum(data, 1e-6)
return data
# --- Custom Transformers ---
def layer_norm(X):
mean = np.mean(X, axis=1, keepdims=True)
std = np.std(X, axis=1, keepdims=True)
return (X - mean) / (std + 1e-8)
def rms_norm(X):
rms = np.sqrt(np.mean(X**2, axis=1, keepdims=True))
return X / (rms + 1e-8)
def log_centering(X):
log_X = np.log1p(X)
mean_log = np.mean(log_X, axis=0, keepdims=True)
return log_X - mean_log
def clr_transform(X):
log_X = np.log(X)
mean_log = np.mean(log_X, axis=1, keepdims=True)
return log_X - mean_log
def decimal_scaling(X):
max_abs = np.max(np.abs(X), axis=0, keepdims=True)
j = np.ceil(np.log10(np.maximum(max_abs, 1e-8)))
return X / (10**j)
def isomap_norm(X):
# Use fewer samples for speed
sample_mask = np.random.choice(X.shape[0], min(300, X.shape[0]), replace=False)
X_sub = X[sample_mask]
iso = Isomap(n_components=1, n_neighbors=15)
X_transformed = iso.fit_transform(X_sub)
# Z-score result
return StandardScaler().fit_transform(X_transformed).flatten()
def plot_points_comparison():
print("Generating data...")
X = generate_visible_data()
feature_idx = 0 # Plot distribution of Feature 0
# Prepare data for plotting
plot_data = []
methods = [
("ORIGINAL DATA", lambda x: x), # Original first
("Z-score (StandardScaler)", StandardScaler()),
("RobustScaler", RobustScaler()),
("Min-Max (0-1)", MinMaxScaler()),
("MaxAbs (-1 to 1)", MaxAbsScaler()),
("Layer Normalization", layer_norm),
("RMSNorm", rms_norm),
("Log-Centering", log_centering),
("CLR Transform", clr_transform),
("Quantile (Normal)", QuantileTransformer(output_distribution='normal', random_state=42)),
("Decimal Scaling", decimal_scaling),
("Unit Vector (L2)", Normalizer()),
("ISOMAP (Manifold)", isomap_norm)
]
print("Transforming data...")
for name, transformer in methods:
try:
if hasattr(transformer, 'fit_transform'):
X_new = transformer.fit_transform(X)
elif callable(transformer):
X_new = transformer(X)
else:
X_new = transformer.transform(X)
# Extract data to plot
if name.startswith("ISOMAP"):
data_points = X_new # Already flattened
elif X_new.ndim == 1:
data_points = X_new
else:
data_points = X_new[:, feature_idx] # Feature 0
# Store for DataFrame
for val in data_points:
plot_data.append({'Method': name, 'Value': val})
except Exception as e:
print(f"Error processing {name}: {e}")
df = pd.DataFrame(plot_data)
# Create Figure
plt.figure(figsize=(16, 12))
# Use a high-contrast palette
# Assign specific color to ORIGINAL DATA (e.g., Red or Black)
palette = sns.color_palette("husl", len(methods))
palette[0] = (0.2, 0.2, 0.2) # Dark Grey/Black for Original
print("Plotting Strip Plot...")
# 1. Strip Plot (Raw Points)
sns.stripplot(x="Value", y="Method", data=df,
size=3, jitter=0.25, alpha=0.6, palette=palette, orient='h', zorder=1)
print("Plotting Box Plot...")
# 2. Box Plot (Summary) - Transparent with colored edges
# Note: seaborn boxplot doesn't support 'edgecolor' easily with hue, so we use standard boxplot
sns.boxplot(x="Value", y="Method", data=df,
whis=1.5, showfliers=False, width=0.5,
boxprops=dict(alpha=0.3),
palette=palette, orient='h', zorder=2)
# Add reference line at 0
plt.axvline(x=0, color='gray', linestyle='--', linewidth=1, alpha=0.5, zorder=0)
# Add title and labels
plt.title("Comparison of Normalization Methods: Distribution & Range\n(Points = Samples | Box = IQR)",
fontsize=20, fontweight='bold', pad=20)
plt.xlabel("Value Magnitude (SymLog Scale)", fontsize=14)
plt.ylabel("")
# Use SymLog scale to show both 0-1 and 0-30 ranges clearly
plt.xscale('symlog', linthresh=1.0)
# Customize grid
plt.grid(True, axis='x', alpha=0.3, which='both')
# Remove spines
sns.despine(left=True, bottom=False)
plt.tight_layout()
output_file = "normalization_points_comparison.png"
plt.savefig(output_file, dpi=150, bbox_inches='tight')
print(f"Saved to {output_file}")
if __name__ == "__main__":
plot_points_comparison()
上面代码运行的效果如下图所示:
 CycleUser
CycleUser