大语言模型似乎很厉害,外行人如果不了解大模型,就可能会觉得这东西很神秘,很了不得,甚至担心什么天人降临统治人类等等。 虽然他可能会告诉你要走路去五十米外的地方洗车,而把车停在原地。
人往往会因为缺乏足够的认知而产生恐惧,实际上稍微从基础层面做一点了解就会发现,这东西并没有那么复杂。 本文的公式内容可能比之前的要多一点,数学直觉稍微钝感的同学可能觉得看着费力。 这不要紧,因为这些公式对于大家来说未必有那么重要,而这个过程的思路,在头脑中能够大概想明白,才是最终重要的。 可以不知道到底是怎么算的,具体公式看不明白写不明白都没事,但是要明白这个过程是怎么样的,要明白为什么这么做,要明白为什么这么做是有效的。 至少这样就不会因为茫然无措而感到恐惧,心里就有底了。真需要细致地去了解这些公式的时候,稍作深入也并不是那么难,到时候再学也来得及。
大模型的能力来源是数据,获得能力的过程要靠训练,而训练过程本质上是在一个高维、复杂的错误率曲面上寻找最低点(即 Loss 最小化)。就像在漆黑的崇山峻岭中寻找谷底,而优化器就是我们手中的指南针和步伐控制器。它决定了我们每次迈出多远、朝哪个方向走,以及遇到坑洼时如何调整姿态。
简单来看,可以把训练大语言模型(LLM)想象成培养一个考试高手的过程。如果说模型架构(如 Transformer)是这个考生的大脑容量和智商上限,海量的训练数据是教材和习题集,那么优化器(Optimizer)就是他所采用的学习方法。这个“学习方法”决定了他在做错题时如何反思:是死记硬背(效率低)、举一反三(效率高),还是针对自己的薄弱环节重点突破(自适应学习)。一个好的优化器,能让模型在同样的时间内学到更多的知识,或者用更少的习题达到同样的考试分数(收敛更快)。
在很长一段时间里,AdamW 都是 LLM 训练的主流选择。然而,随着模型规模的不断膨胀和对训练效率的极致追求,名为 Muon 的新型优化器横空出世,能以更少的步数达到相同的效果。这回咱们就看看优化器的简单来历以及特点等等。
一、优化器的基石:从 SGD 到自适应
1. 为什么“随机梯度下降”能有用?(SGD)
想象你在山上迷路了,周围大雾弥漫(看不清全貌),你想下山(找 Loss 最低点)。 你唯一能做的是:用脚探一探周围哪里最陡。 如果脚下的路是向北向下倾斜的,那你往北走一步,大概率海拔会降低。 这就是 SGD(随机梯度下降) 的核心思想: * 梯度(Gradient):就是“坡度”和“方向”。 * 下降(Descent):沿着坡最陡的方向往下走。 * 随机(Stochastic):因为山太大了(数据太多),我们没法一次性把整座山都测绘一遍。我们每次只随机挑一小块地(Mini-batch)来探路。虽然有时候这块地的坡度可能带有误导性(比如只是个小坑),但只要次数够多,大方向总体是向下的。
$$ W_{t+1} = W_t - \eta \cdot \nabla L(W_t) $$
2. 什么是“动量”?(Momentum)
SGD 有个大问题:它没有“惯性”。 如果山谷是狭长的(像一个U型管),SGD 可能会在两边的峭壁上来回撞(震荡),而不能顺着谷底快速流下去。或者遇到一个小坑(局部最优),它可能就停在坑底不动了,因为它只看脚下,不看趋势。
于是我们引入了 动量(Momentum),想象把下山的人换成一个 大铁球。 * 惯性保持:当球滚下来时,它积累了速度(动量)。即使遇到一个小坡(梯度的反方向),靠着之前的惯性,它也能冲过去。 * 加速前进:如果一直是下坡路,球会越滚越快,比每一步都重新起步的 SGD 快得多。
在数学上,就是把“上一步的更新方向”加个系数(比如 0.9),叠加上“当前的梯度”。 $$ v_t = \gamma v_{t-1} + \eta \nabla L(W) $$ $$ W = W - v_t $$
3. 什么是“自适应步长”?(Adaptive Learning Rate)
SGD 和 Momentum 还有一个共同的痛点:所有参数用同一个步长(学习率)。 但这在深度学习中很不合理。有些参数(比如Embedding层中常见词的权重)经常更新,对应的坡度很陡,如果步子太大容易扯着蛋甚至直接掉落“飞”出去;有些参数(生僻词的权重)很少更新,坡度很平,如果步子太小简直像蜗牛原地小步爬。
自适应步长(如 RMSProp, AdaGrad)的思想是:给每个参数配一双特制的鞋。 * 陡坡穿小鞋:如果某个参数历史梯度的波动很大(平方和很大),说明这里地形险恶,我们要把它的学习率除以一个大数,让它走慢点,稳一点。 * 平地穿大鞋:如果某个参数历史梯度一直很小,说明这里是一马平川,我们要把它的学习率除以一个小数(相当于放大),让它大步流星往前冲。
这就是 AdamW 中 $v_t$(二阶矩)的作用:记录每个参数“过去有多颠簸”,然后据此调整它当下的步长。
4. 进化之路:从 SGD 到 Adam 的家谱
了解了上面三个概念,我们就能串起整个优化器的进化史:
- SGD:只有方向,没有惯性,步长固定。
- 缺点:慢,容易卡在鞍点。
- SGD + Momentum:加上了“惯性”。
- 进化点:解决了震荡和鞍点问题,跑得快了。
- AdaGrad:加上了“自适应步长”(累计所有历史梯度的平方)。
- 进化点:解决了稀疏数据(生僻词)更新难的问题。
- 缺点:因为是“累计”历史,分母会越来越大,训练到后期步长几乎为0,学不动了。
- RMSProp:改进版 AdaGrad(只看最近一段时间的梯度平方)。
- 进化点:解决了 AdaGrad 训练后期熄火的问题。
- Adam (Adaptive Moment Estimation):集大成者。
- Adam = Momentum + RMSProp
- 它既用了 Momentum(一阶矩)来保持方向惯性,又用了 RMSProp(二阶矩)来自适应调整步长。可以说它既有“速度”,又有“路感”。
二、工业标准:AdamW(Adaptive Moment Estimation with Weight Decay)
AdamW 是 Adam 优化器的改进版,它结合了动量(一阶矩)和自适应步长(二阶矩),并正确地解耦了权重衰减(Weight Decay)。它是目前训练 GPT、Llama 等大模型的默认选择。
1. 核心机制
AdamW 维护两个状态变量: * $m_t$(一阶矩):梯度的指数移动平均(类似动量)。 * $v_t$(二阶矩):梯度平方的指数移动平均(用于衡量梯度的波动大小)。
2. 算法步骤
对于每个参数 $w$,在第 $t$ 步:
- 计算梯度 $g_t$。
- 更新一阶矩(动量): $$ m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t $$
- 更新二阶矩(自适应缩放因子): $$ v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 $$
- 偏差修正(初期 $m, v$ 偏向 0,需放大): $$ \hat{m}_t = m_t / (1 - \beta_1^t), \quad \hat{v}_t = v_t / (1 - \beta_2^t) $$
- 参数更新(关键步骤): $$ w_{t+1} = w_t - \eta \left( \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} + \lambda w_t \right) $$ 其中 $\frac{1}{\sqrt{\hat{v}_t}}$ 实现了自适应步长:梯度大的参数更新步幅缩小,梯度小的参数步幅放大。$\lambda w_t$ 是解耦后的权重衰减。
3. 优劣势分析
- 优势:
- 极度稳健:几乎适用于任何类型的网络(CNN, RNN, Transformer),超参数(lr=1e-3/1e-4)有公认的默认值。
- 自适应性:无需为每个层手动调整学习率。
- 劣势:
- 显存占用高:需要为每个参数存储 $m$ 和 $v$ 两个状态,显存占用是参数量的 2 倍(如果是 FP32 状态,甚至更多)。
- 计算偏内存密集:主要是逐元素的加减乘除,受限于显存带宽(Memory Bandwidth Bound)。
三、新晋选手:Muon(Momentum Update Orthogonalized Newton)
Muon 是专门针对 Transformer 中的二维权重矩阵(如 Linear 层的 $W$)设计。它的核心洞见是:将参数更新约束为正交变换,利用矩阵的整体结构而非逐元素调整。
1. 核心机制
Muon 不再像 AdamW 那样逐个元素地看梯度的“方差”,而是将整个权重矩阵视为一个整体。它通过 Newton-Schulz 迭代 将梯度的动量矩阵进行正交化(Orthogonalization)。
这意味着 Muon 的更新步长在所有方向上是“均匀”的(基于谱范数),这允许模型使用更大的学习率,从而在训练初期快速穿越平坦区域。
2. 算法步骤
Muon 通常只用于 $\ge 2$ 维的张量(如 $W_{Q}, W_{K}, W_{V}$),而 1 维参数(如 LayerNorm, Bias)仍使用 AdamW。
- 计算梯度 $G$。
- 更新动量: $$ M_t = \beta M_{t-1} + G $$
- 正交化(Newton-Schulz Iteration): 为了得到 $M_t$ 的正交化版本 $\mathcal{O}(M_t)$,我们不使用昂贵的 SVD,而是用迭代法近似。 令 $X_0 = M_t / (|M_t|F + \epsilon)$(归一化)。 循环迭代(通常 5 次): $$ X X_k (3I - X_k^T X_k) $$ 最终得到 $U = X_K$。} = \frac{1}{2
- 参数更新: $$ W_{t+1} = W_t - \eta \cdot U \cdot \sigma(W_t) $$ (通常还会根据权重自身的 RMS 进行缩放)
3. 优劣势分析
- 优势:
- 收敛极快:正交更新使得优化器敢于迈大步,样本效率(Sample Efficiency)显著高于 AdamW。
- 硬件友好:核心操作是矩阵乘法(MatMul),能充分利用 GPU 的 Tensor Cores,将负载从内存带宽转移到算力上。
- 显存占用较低:仅需存储动量 $M$(1 倍状态),且 Newton-Schulz 过程不需要额外的持久化状态。
- 劣势:
- 实现复杂:需要混合优化策略(Muon 处理矩阵 + AdamW 处理向量)。
- 超参敏感:Newton-Schulz 的迭代次数、动量系数等可能需要针对特定模型微调。
- 数值稳定性:如果矩阵条件数极差,迭代可能不稳定。
四、AdamW vs. Muon 对比
| 维度 | AdamW | Muon |
|---|---|---|
| 设计哲学 | 逐元素自适应:每个参数独立调整步长,基于历史梯度的方差。 | 矩阵整体正交:保留梯度的方向结构,去除幅度影响,基于谱范数。 |
| 状态量 (State) | 2 个 ($m, v$) | 1 个 ($m$) |
| 计算瓶颈 | 显存带宽 (Memory Bound):大量的 Element-wise 操作。 | 算力 (Compute Bound):大量的 Matrix Multiplication。 |
| 适用场景 | 通用,所有参数。 | 仅限 2D+ 权重矩阵(Linear, Embeddings)。 |
| 收敛速度 | 稳健,标准速度。 | 激进,在从零训练 LLM 时往往更快。 |
| 典型应用 | 绝大多数现有模型 (GPT-4, Llama 3)。 | 追求极致效率的开源小模型 (NanoGPT speedruns)。 |
五、可视化对比
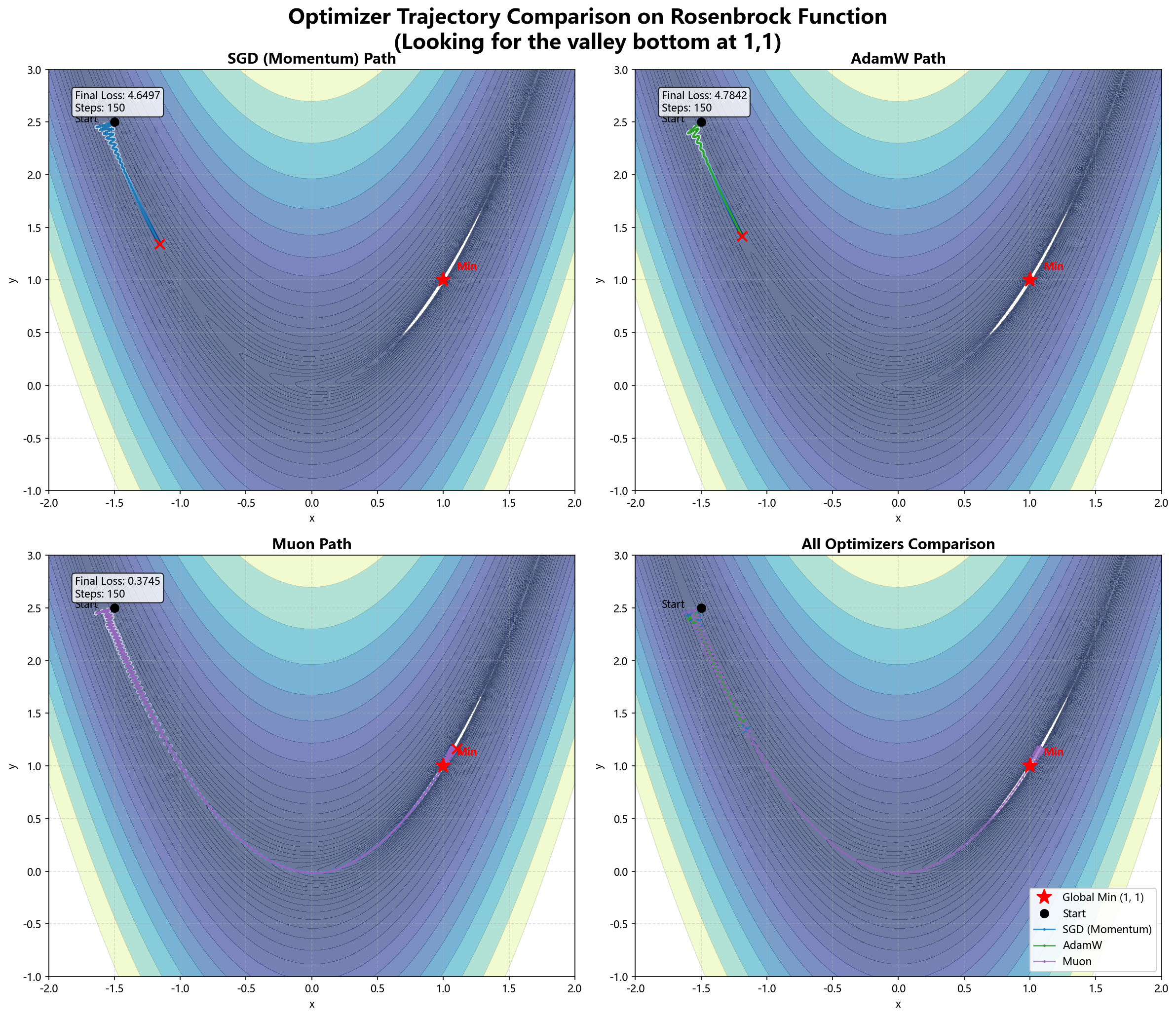
为了直观展示两者的区别,我们在经典的 Rosenbrock 函数(香蕉函数)上模拟了 SGD、AdamW 和 Muon 的寻优路径。
- SGD:在山谷壁上震荡,前进缓慢。
- AdamW:利用二阶矩快速适应了不同方向的曲率,直奔谷底。
- Muon(模拟版):通过正交化(在低维下近似为单位步长),路径更加平滑且直接。
(注:真实 Muon 威力在于高维矩阵的谱结构处理,此处仅为 2D 轨迹示意)
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import platform
# Configure fonts for Chinese support
system = platform.system()
if system == 'Windows':
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimHei', 'Arial']
elif system == 'Darwin':
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'PingFang SC']
else:
plt.rcParams['font.sans-serif'] = ['WenQuanYi Micro Hei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
def rosenbrock(x, y, a=1, b=100):
return (a - x)**2 + b * (y - x**2)**2
def grad_rosenbrock(x, y, a=1, b=100):
dx = -2 * (a - x) - 4 * b * x * (y - x**2)
dy = 2 * b * (y - x**2)
return np.array([dx, dy])
# Optimizer Implementations
class SGD:
def __init__(self, lr=0.001, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = np.zeros(2)
def step(self, params, grads):
self.v = self.momentum * self.v - self.lr * grads
return params + self.v
class AdamW:
def __init__(self, lr=0.01, beta1=0.9, beta2=0.999, eps=1e-8, weight_decay=0.01):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
self.wd = weight_decay
self.m = np.zeros(2)
self.v = np.zeros(2)
self.t = 0
def step(self, params, grads):
self.t += 1
# Weight decay
params = params - self.lr * self.wd * params
# Adam
self.m = self.beta1 * self.m + (1 - self.beta1) * grads
self.v = self.beta2 * self.v + (1 - self.beta2) * grads**2
m_hat = self.m / (1 - self.beta1**self.t)
v_hat = self.v / (1 - self.beta2**self.t)
return params - self.lr * m_hat / (np.sqrt(v_hat) + self.eps)
class Muon:
def __init__(self, lr=0.02, momentum=0.95, nesterov=True, ns_steps=5):
self.lr = lr
self.momentum = momentum
self.nesterov = nesterov
self.ns_steps = ns_steps
self.m = np.zeros(2)
def newton_schulz(self, M):
# M is shape (1, 2) or (2,) treated as (1, 2)
# For a vector, this is effectively normalization, but let's simulate the matrix steps
# Shape handling
if M.ndim == 1:
M = M.reshape(1, -1)
# Normalization (Spectral norm approx via Frobenius for small matrix)
# X = M / (||M|| + eps)
norm = np.linalg.norm(M) + 1e-8
X = M / norm
# Newton-Schulz Iteration
# X_{k+1} = 0.5 * X_k * (3I - X_k^T * X_k)
# Note: For non-square matrices A (m x n), we use A * (3I - A^T A) or (3I - A A^T) * A depending on dimensions
# Here 1x2, let's use the standard form for whitening: X * (3I - X.T @ X)
# Wait, if X is 1x2, X.T @ X is 2x2. X @ X.T is 1x1.
# The iteration converges to a matrix with singular values all 1.
for _ in range(self.ns_steps):
# For 1x2:
# A = X (1x2)
# B = 3I - X^T @ X (2x2)
# This direction is computationally heavier for 1x2.
# Alternative: X_{k+1} = 1.5 * X_k - 0.5 * X_k @ (X_k.T @ X_k)
# Actually for vector v, v^T v is a scalar if column vector, but here row.
XTX = X.T @ X # (2, 2)
eye = np.eye(2)
X = 0.5 * X @ (3 * eye - XTX)
return X.flatten()
def step(self, params, grads):
self.m = self.momentum * self.m + grads
if self.nesterov:
v = self.momentum * self.m + grads
else:
v = self.m
# Orthogonalize v using Newton-Schulz
update = self.newton_schulz(v)
# Scale by root-mean-square of params (often used in Muon implementations for consistency)
# or just standard LR. Original Muon paper/impl often scales by max(1, rms(params))
# Let's stick to simple LR for visualization
return params - self.lr * update
def visualize():
# Setup plot
fig, ax = plt.subplots(figsize=(10, 8))
# Generate meshgrid for contour
x = np.linspace(-2, 2, 400)
y = np.linspace(-1, 3, 400)
X, Y = np.meshgrid(x, y)
Z = rosenbrock(X, Y)
# Plot contours (log scale for better visibility)
ax.contour(X, Y, Z, levels=np.logspace(-1, 3, 30), cmap='gray_r', alpha=0.4)
ax.plot(1, 1, 'r*', markersize=15, label='Global Min (1, 1)')
# Starting point
start_pos = np.array([-1.5, 2.5])
# Run Optimizers
optimizers = [
('SGD (Momentum)', SGD(lr=0.0005, momentum=0.9), 'blue'),
('AdamW', AdamW(lr=0.05, weight_decay=0.01), 'green'),
('Muon', Muon(lr=0.05, momentum=0.95), 'purple')
]
steps = 200
for name, opt, color in optimizers:
path = [start_pos]
params = start_pos.copy()
for _ in range(steps):
grads = grad_rosenbrock(params[0], params[1])
params = opt.step(params, grads)
path.append(params)
path = np.array(path)
ax.plot(path[:, 0], path[:, 1], '.-', color=color, label=name, alpha=0.8, linewidth=1.5, markersize=3)
# Mark end
ax.plot(path[-1, 0], path[-1, 1], 'o', color=color)
ax.set_title("优化器寻优路径对比: SGD vs AdamW vs Muon\n(Loss: Rosenbrock Function)", fontsize=14)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.legend()
ax.grid(True, linestyle='--', alpha=0.3)
plt.tight_layout()
plt.savefig('optimizer_comparison.png', dpi=150)
print("Optimization comparison plot saved to optimizer_comparison.png")
if __name__ == "__main__":
visualize()
六、结语
世间安得双全法?优化器的选择本质上是在计算效率(FLOPs vs Memory)与收敛质量之间做权衡。 在硬件资源有限的情况下,我们倾向于选择计算效率更高的优化器;而在硬件资源充足的情况下,我们则更倾向于选择收敛质量更高的优化器。 AdamW 凭借其稳健性,依然是当今 LLM 训练的“压舱石”。而 Muon 则像是一辆激进的赛车,通过更针对性设计的数学工具(牛顿迭代、正交化)挖掘硬件潜力,试图在训练速度上有所改进。
随着 GPU 架构向着“高算力、相对低带宽”演进,类似 Muon 这样计算密集型(Compute-Heavy)的优化器可能会越来越受到青睐。理解它们背后的数学直觉,能帮助更好地理解大模型。
 CycleUser
CycleUser