神经网络里面的重要部分就是激活函数,它决定了神经网络中每层的输出。激活函数的作用是引入非线性因素,使得神经网络能够逼近任意复杂的非线性函数。
从简单分段线性(ReLU)到平滑概率型(GELU)再到门控非线性(SwiGLU)的演进,反映了深度学习模型,尤其是大语言模型,演化上的一个趋势,更强表达能力和更好优化特性。
本文简单介绍 ReLU、GELU 和 SwiGLU 三种激活函数,并给出 Python 实现和可视化(基于 matplotlib)。
激活函数简介
1. ReLU(Rectified Linear Unit)
ReLU 是最广泛使用的激活函数之一,其定义简单且计算高效:
$$ \text{ReLU}(x) = \max(0, x) = \begin{cases} x, & x > 0 \ 0, & x \leq 0 \end{cases} $$
优点包括: - 计算简单,加速训练; - 缓解梯度消失问题(对正输入梯度恒为 1)。
缺点: - 存在“死神经元”问题(负输入梯度为 0,无法更新)。
2. GELU(Gaussian Error Linear Unit)
GELU 是一种平滑、非单调的激活函数,被广泛用于 Transformer 架构(如 BERT、GPT)。其定义基于标准正态分布的累积分布函数(CDF):
$$ \text{GELU}(x) = x \cdot \Phi(x) = x \cdot \frac{1}{2} \left[1 + \operatorname{erf}\left(\frac{x}{\sqrt{2}}\right)\right] $$
其中 $\Phi(x)$ 是标准正态分布的 CDF,$\operatorname{erf}(\cdot)$ 是误差函数。
近似形式(常用于实现): $$ \text{GELU}(x) \approx 0.5x\left(1 + \tanh\left[\sqrt{\frac{2}{\pi}}(x + 0.044715x^3)\right]\right) $$
GELU 的优势在于: - 平滑可导,有利于优化; - 融合了 dropout 与非线性的思想(通过概率加权)。
3. SwiGLU(Swish-Gated Linear Unit)
SwiGLU 是一种门控激活函数,结合了 Swish 激活与 GLU(Gated Linear Unit) 结构,在现代大语言模型(如 Qwen、PaLM、LLaMA-2)中表现优异。
首先定义 Swish 函数: $$ \text{Swish}(x) = x \cdot \sigma(\beta x) $$ 其中 $\sigma(z) = \frac{1}{1 + e^{-z}}$ 是 Sigmoid 函数,$\beta$ 通常设为 1。
SwiGLU 将输入 $x$ 分成两部分(或使用两个线性投影 $W$ 和 $V$),然后应用门控机制:
$$ \text{SwiGLU}(x) = \text{Swish}(xW) \otimes (xV) $$
若仅考虑标量输入(用于可视化),可简化为: $$ \text{SwiGLU}(x) = \text{Swish}(x) \cdot x = x \cdot \sigma(x) \cdot x = x^2 \cdot \sigma(x) $$
注:严格来说,SwiGLU 需要两个独立的线性变换,但为了可视化目的,我们采用上述简化形式以展示其非线性特性。
SwiGLU 的优势: - 引入门控机制,增强表达能力; - 实验表明在语言建模任务中优于 ReLU 和 GELU。
可视化代码(Python + Matplotlib)
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import erf
# 定义激活函数
def relu(x):
return np.maximum(0, x)
def gelu(x):
return 0.5 * x * (1 + erf(x / np.sqrt(2)))
def swish(x, beta=1.0):
return x / (1 + np.exp(-beta * x))
def swiglu_simplified(x):
# 简化版:SwiGLU(x) ≈ Swish(x) * x
return swish(x) * x
# 生成 x 值
x = np.linspace(-4, 4, 400)
# 计算 y 值
y_relu = relu(x)
y_gelu = gelu(x)
y_swiglu = swiglu_simplified(x)
# 绘图
plt.figure(figsize=(10, 6))
plt.plot(x, y_relu, label=r'$\text{ReLU}(x)$', linewidth=2)
plt.plot(x, y_gelu, label=r'$\text{GELU}(x)$', linewidth=2)
plt.plot(x, y_swiglu, label=r'$\text{SwiGLU}_{\text{simplified}}(x) = x \cdot \sigma(x) \cdot x$', linewidth=2)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid(True, linestyle='--', alpha=0.6)
plt.xlim(-4, 4)
plt.ylim(-1, 4)
plt.xlabel(r'$x$', fontsize=14)
plt.ylabel(r'$f(x)$', fontsize=14)
plt.title('Comparison of ReLU, GELU, and SwiGLU Activation Functions', fontsize=16)
plt.legend(fontsize=12)
plt.tight_layout()
plt.show()
上面的代码可视化效果如下所示:
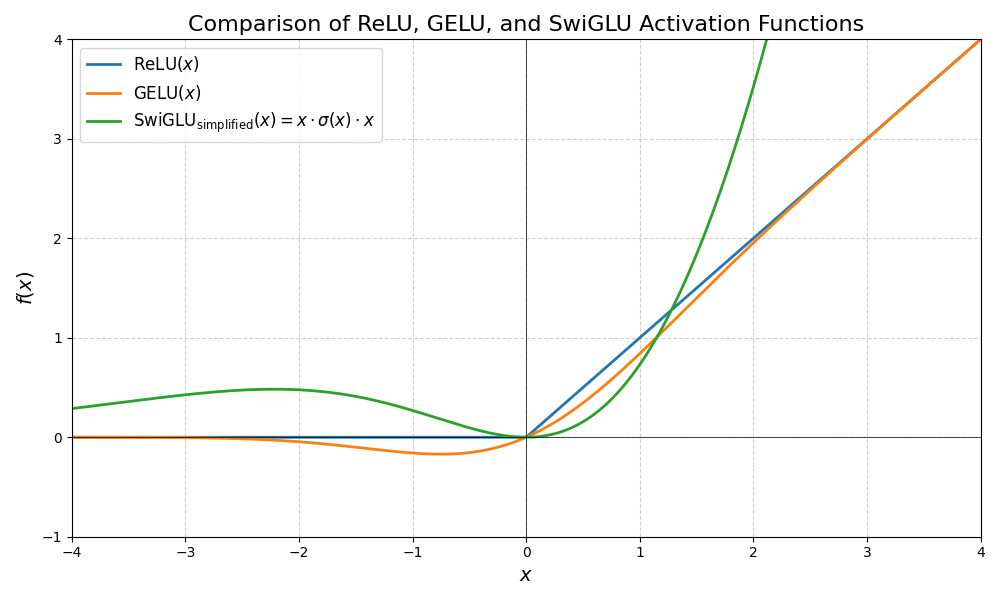
可视化说明
- ReLU:在 $x > 0$ 时为线性,$x \leq 0$ 时恒为 0。
- GELU:平滑曲线,在负区有微小输出,正区近似线性但带轻微弯曲。
- SwiGLU(简化):在正区增长快于线性(因含 $x^2$ 项),负区趋近于 0 但非完全截断。实际 SwiGLU 使用两个不同的线性投影,因此其形状依赖于权重。此处简化仅为展示函数形态。
 CycleUser
CycleUser