拉普拉斯的介绍
皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace,1749-1827)是法国数学家、天文学家和物理学家,被誉为“法国的牛顿”。他在天体力学、概率论与数学物理领域奠定了许多基础,也推动了偏微分方程的发展。
拉普拉斯算子是数学物理中最核心的微分算子之一。它把一个标量场映射到另一个标量场,用来度量“某点的数值相对于周围平均值的偏离程度”,从而反映函数的局部形态(凸、凹或平坦)。
核心思想:设 $f$ 是定义在区域 $\Omega$ 上的函数,$x_0 \in \Omega$。用 $B_r(x_0)$ 表示以 $x_0$ 为中心、半径为 $r$ 的球,$\bar{f}_r$ 表示 $f$ 在球面上的平均值。则:
$$\nabla^2 f(x_0) = \lim_{r \to 0} \frac{2d}{r^2} \left( \bar{f}_r - f(x_0) \right)$$
其中 $d$ 是空间维数,这个系数保证了不同维度下的尺度一致性。
物理诠释: - 若 $\nabla^2 f(x_0) > 0$,说明 $f(x_0)$ 低于周围平均值,该点像“谷底” - 若 $\nabla^2 f(x_0) < 0$,说明 $f(x_0)$ 高于周围平均值,该点像“峰顶” - 若 $\nabla^2 f(x_0) = 0$,说明 $f(x_0)$ 与周围平均值相当,局部近似“平坦”
拉普拉斯算子的来源
拉普拉斯算子的雏形最早出现在拉普拉斯对天体引力势的研究中。1782 年,他研究行星引力场时发现,引力势函数满足一个特殊的二阶偏微分方程:
$$\frac{\partial^2 V}{\partial x^2} + \frac{\partial^2 V}{\partial y^2} + \frac{\partial^2 V}{\partial z^2} = 0$$
这就是著名的拉普拉斯方程,而左端的微分算子后来被命名为拉普拉斯算子。它描述了“无源场”中的势函数特性,是许多物理问题的核心方程。
引力势的例子:设质量为 $m$ 的质点位于原点,其引力势为 $V = -\frac{Gm}{r}$,其中 $r = \sqrt{x^2+y^2+z^2}$。在 $r > 0$ 的区域内有 $\nabla^2 V = 0$,对应“真空中的调和势”。
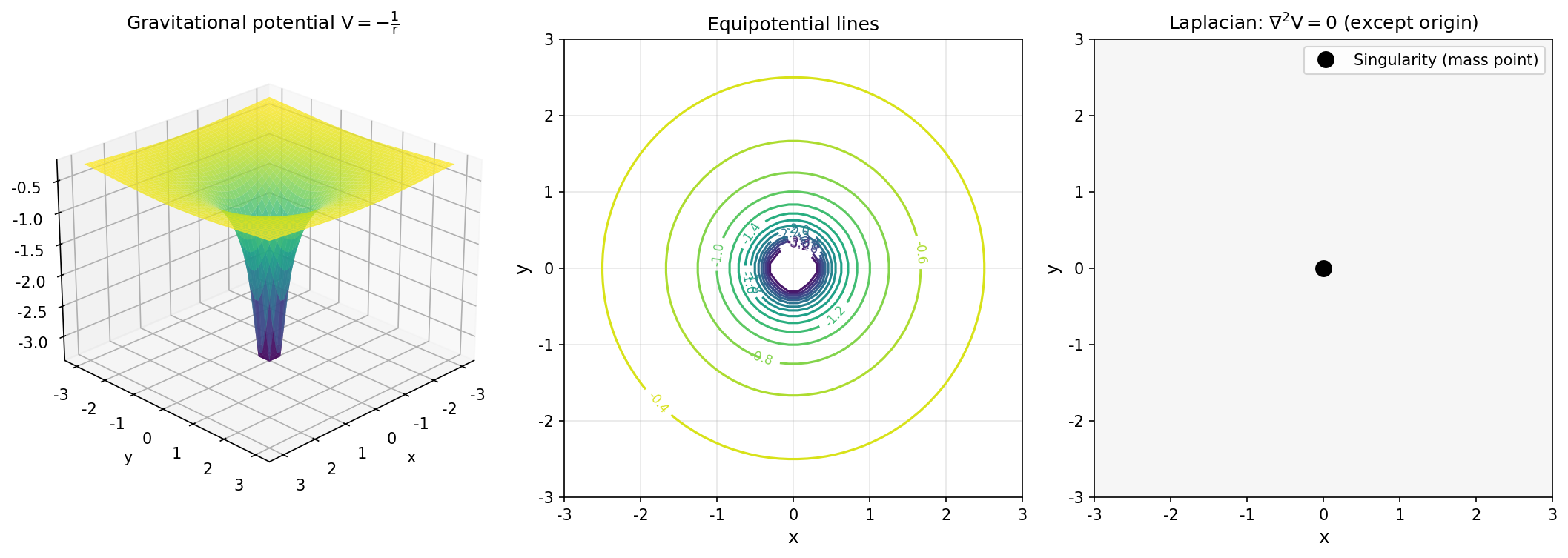
图1:引力势 $V = -1/r$ 的可视化。左图:三维势能曲面。中图:等势线。右图:拉普拉斯为零(除去原点奇点)。
记号约定:拉普拉斯算子常见的写法如下,三者等价,但侧重语境不同。
| 记法 | 来源 | 使用场景 |
|---|---|---|
| $\nabla^2$ | 哈密顿引入 | 物理学、工程学 |
| $\Delta$ | 欧洲传统 | 数学文献 |
| $\operatorname{div} \nabla$ | 算子形式 | 强调散度-梯度关系 |
梯度
为了理解拉普拉斯算子,先从梯度开始。对标量函数 $f: \mathbb{R}^d \to \mathbb{R}$,梯度定义为:
$$\nabla f = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_d} \right)$$
几何意义:梯度是一个向量,方向指向函数增长最快的方向,模长给出最大增长率。
数值示例:设 $f(x, y) = x^2 + y^2$,则
$$\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) = (2x, 2y)$$
在点 $(1, 2)$ 处,$\nabla f = (2, 4)$。
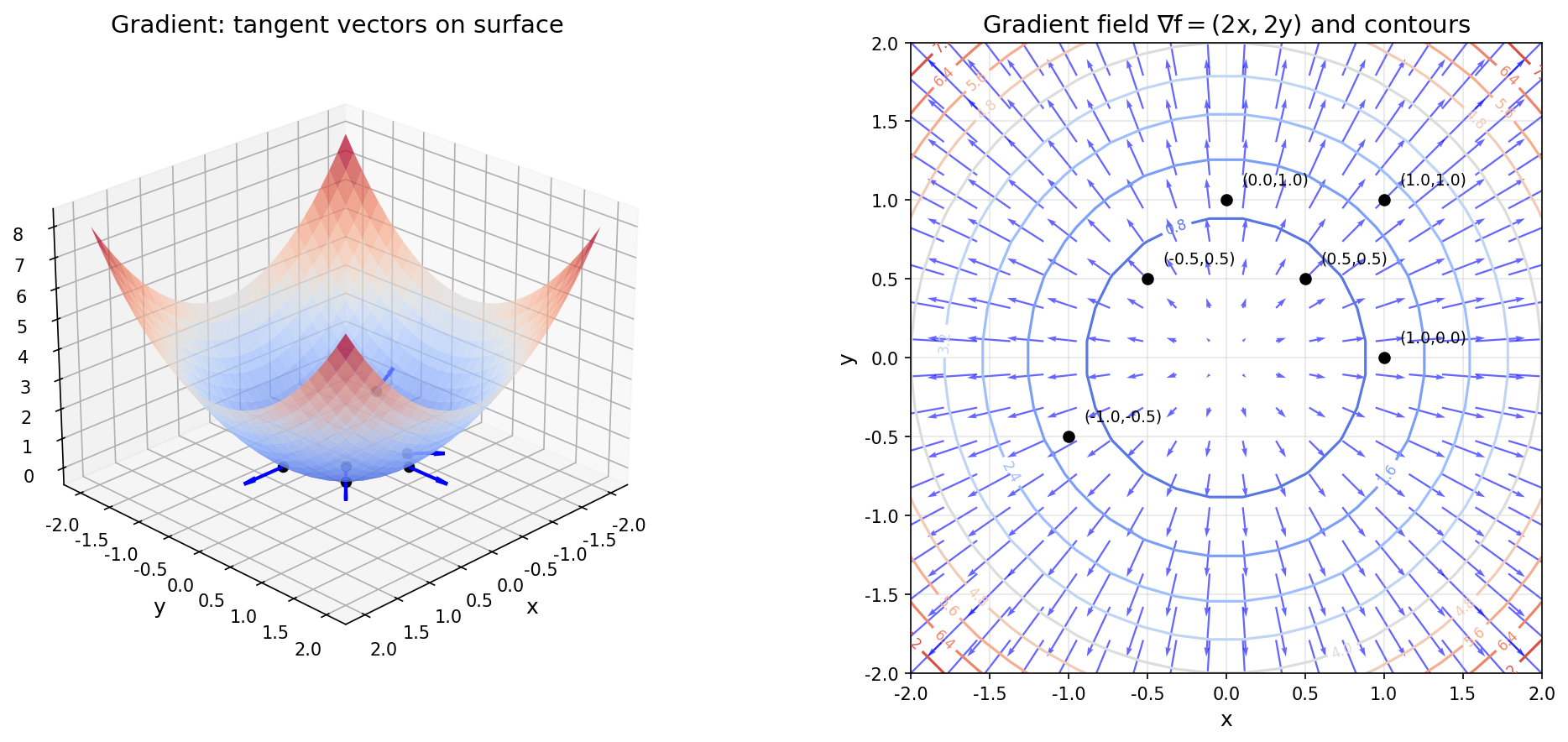
图2:梯度可视化。左图:三维曲面 $f(x,y)=x^2+y^2$ 上的梯度向量(蓝色箭头),梯度沿切平面指向函数增长最快的方向。右图:二维平面上的梯度向量场与等高线,梯度始终垂直于等高线。
关键性质: - 梯度方向:函数增长最快的方向 - 梯度模长:最大变化率 - 梯度与等高线垂直
散度
接着看散度。对向量场 $\mathbf{F} = (F_1, F_2, \ldots, F_d)$,散度定义为:
$$\nabla \cdot \mathbf{F} = \frac{\partial F_1}{\partial x_1} + \frac{\partial F_2}{\partial x_2} + \cdots + \frac{\partial F_d}{\partial x_d}$$
物理意义:散度刻画向量场在某点“发散或汇聚”的强度。正散度表示该点像“源”(向外发散),负散度表示该点像“汇”(向内汇聚)。
数值示例:设 $\mathbf{F} = (x^2, y^2, z^2)$,则
$$\nabla \cdot \mathbf{F} = \frac{\partial (x^2)}{\partial x} + \frac{\partial (y^2)}{\partial y} + \frac{\partial (z^2)}{\partial z} = 2x + 2y + 2z$$
在点 $(1, 2, 3)$ 处,$\nabla \cdot \mathbf{F} = 2 + 4 + 6 = 12$。
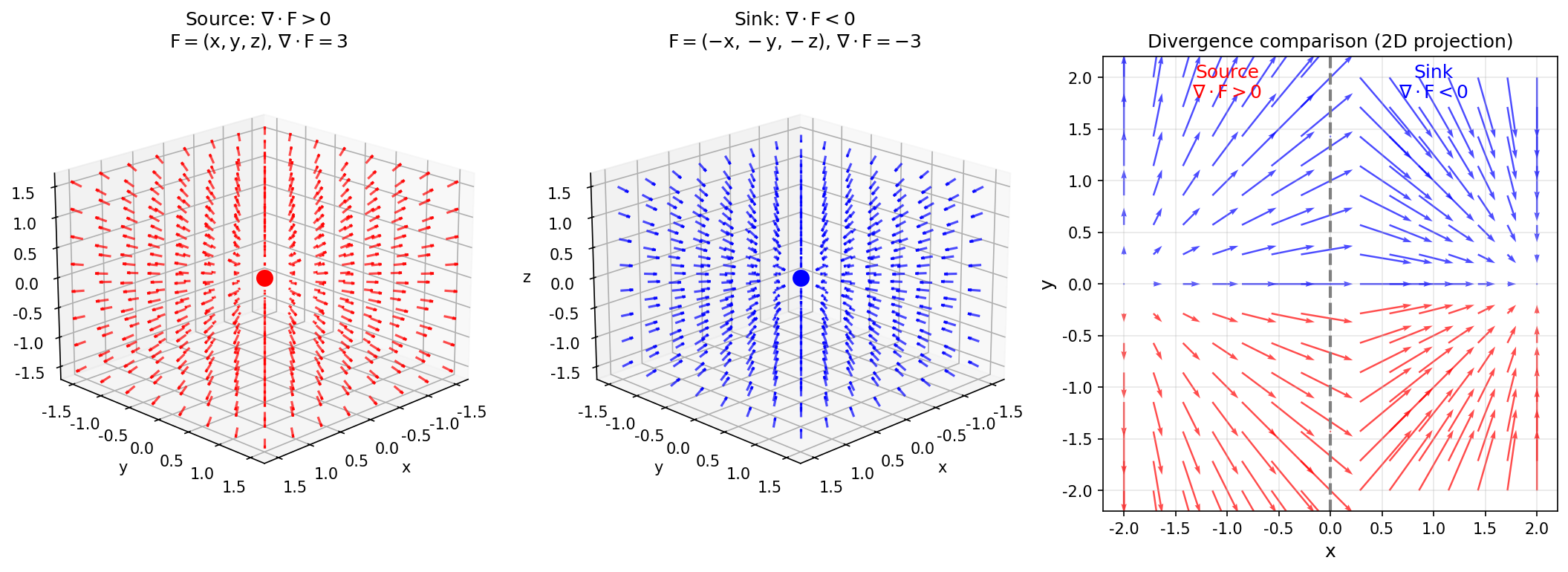
图3:散度可视化。左图:源场 $\mathbf{F}=(x,y,z)$,所有向量向外发散,散度为正($\nabla\cdot\mathbf{F}=3$)。中图:汇场 $\mathbf{F}=(-x,-y,-z)$,所有向量向内汇聚,散度为负($\nabla\cdot\mathbf{F}=-3$)。右图:二维投影对比,左侧为源、右侧为汇。
关键性质: - 散度为正:该点是"源",物质向外扩散 - 散度为负:该点是"汇",物质向内汇聚 - 散度为零:该点既不产生也不消灭物质
拉普拉斯算子
定义
拉普拉斯算子就是“梯度的散度”:
$$\nabla^2 f = \nabla \cdot (\nabla f)$$
展开即得:
$$\nabla^2 f = \frac{\partial^2 f}{\partial x_1^2} + \frac{\partial^2 f}{\partial x_2^2} + \cdots + \frac{\partial^2 f}{\partial x_d^2} = \sum_{i=1}^{d} \frac{\partial^2 f}{\partial x_i^2}$$
这是一个二阶线性微分算子,把标量函数映射为标量函数。
梯度、散度与拉普拉斯的关系
拉普拉斯算子本质上是梯度与散度的复合,可以理解为“先看增长方向,再看这些方向如何发散”:
$$\nabla^2 f = \nabla \cdot (\nabla f)$$
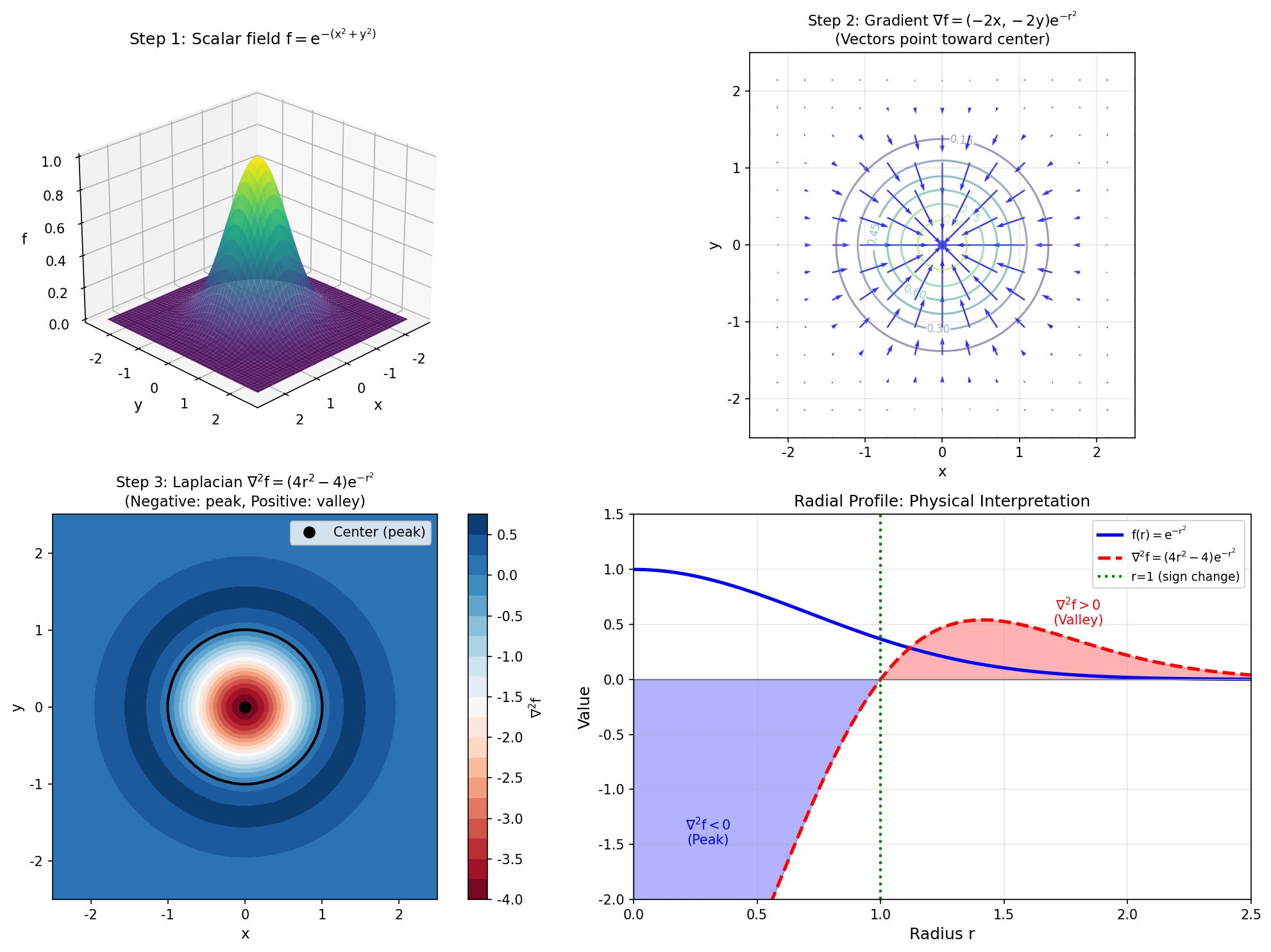
图4:拉普拉斯算子的定义过程。Step 1:标量场 $f$。Step 2:求梯度得到向量场 $\nabla f$。Step 3:求散度得到标量场 $\nabla^2 f$。
关键洞察: - 梯度:标量场变为向量场,描述局部上升最快方向 - 散度:向量场变为标量场,描述局部“源/汇”强度 - 拉普拉斯:标量 → 向量 → 标量,体现“局部偏离平均值”的程度 - 拉普拉斯完成闭环:$f \to\nabla f \to\nabla \cdot (\nabla f) =\nabla^2 f$(标量 → 向量 → 标量)
以热传导为例,设 $f$ 表示温度场: - $\nabla f$ 是温度梯度,指向温度增加最快的方向 - 热流 $\mathbf{q} = -k \nabla f$(傅里叶定律:热量从高温流向低温) - $\nabla \cdot \mathbf{q} = -k \nabla^2 f$ 描述热流的局部汇聚或发散 - 若 $\nabla^2 f > 0$,热量汇聚(温度低于周围平均),温度上升 - 若 $\nabla^2 f < 0$,热量发散(温度高于周围平均),温度下降
数值示例:设 $f(x, y, z) = x^2 + y^2 + z^2$
第一步:求梯度
$$\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right) = (2x, 2y, 2z)$$
第二步:求散度
因此 $\nabla^2 f = 6 > 0$,表示 $f$ 在每点都低于周围平均值,是典型的凸函数。
一维二维三维情况
在一维情形,拉普拉斯算子简化为二阶导数:
几何意义:二阶导数反映函数的“凹凸性”。
数值示例:
- $f(x) = x^2$:$\nabla^2 f = f''(x) = 2 > 0$,函数"凹"(开口向上)
- $f(x) = -x^2$:$\nabla^2 f = f''(x) = -2 < 0$,函数"凸"(开口向下)
- $f(x) = x^3 - 3x$:$\nabla^2 f = f''(x) = 6x$,在 $x > 0$ 时凹,在 $x < 0$ 时凸
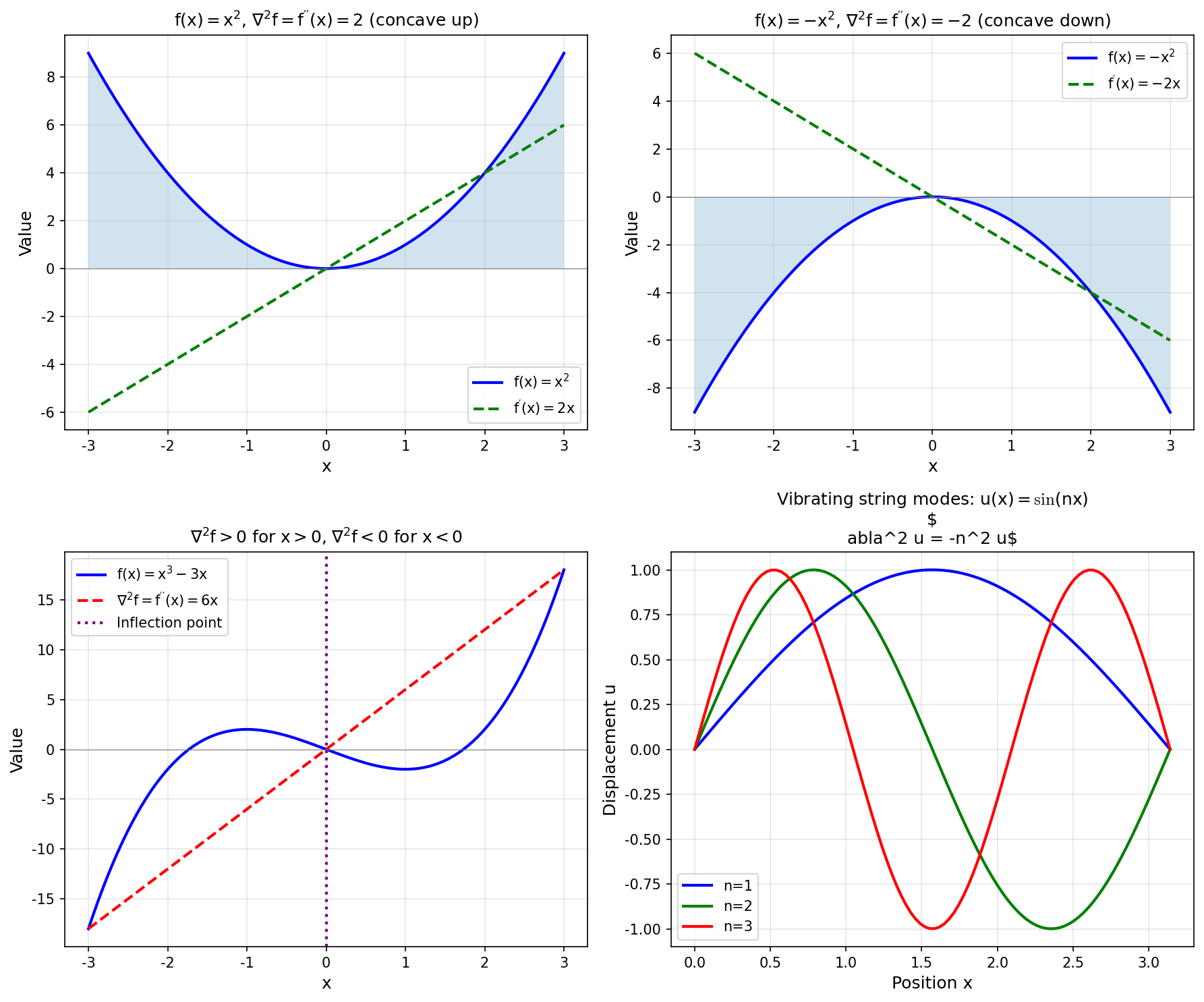
物理解释:考虑一根张紧的弦,设 $u(x, t)$ 表示弦在位置 $x$、时刻 $t$ 的位移。弦的振动方程为:
其中 $c$ 是波速。一维拉普拉斯算子描述弦的“弯曲程度”,对应恢复力的强弱。
在二维情形,使用笛卡尔坐标 $(x, y)$:
$$\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$$
数值示例:
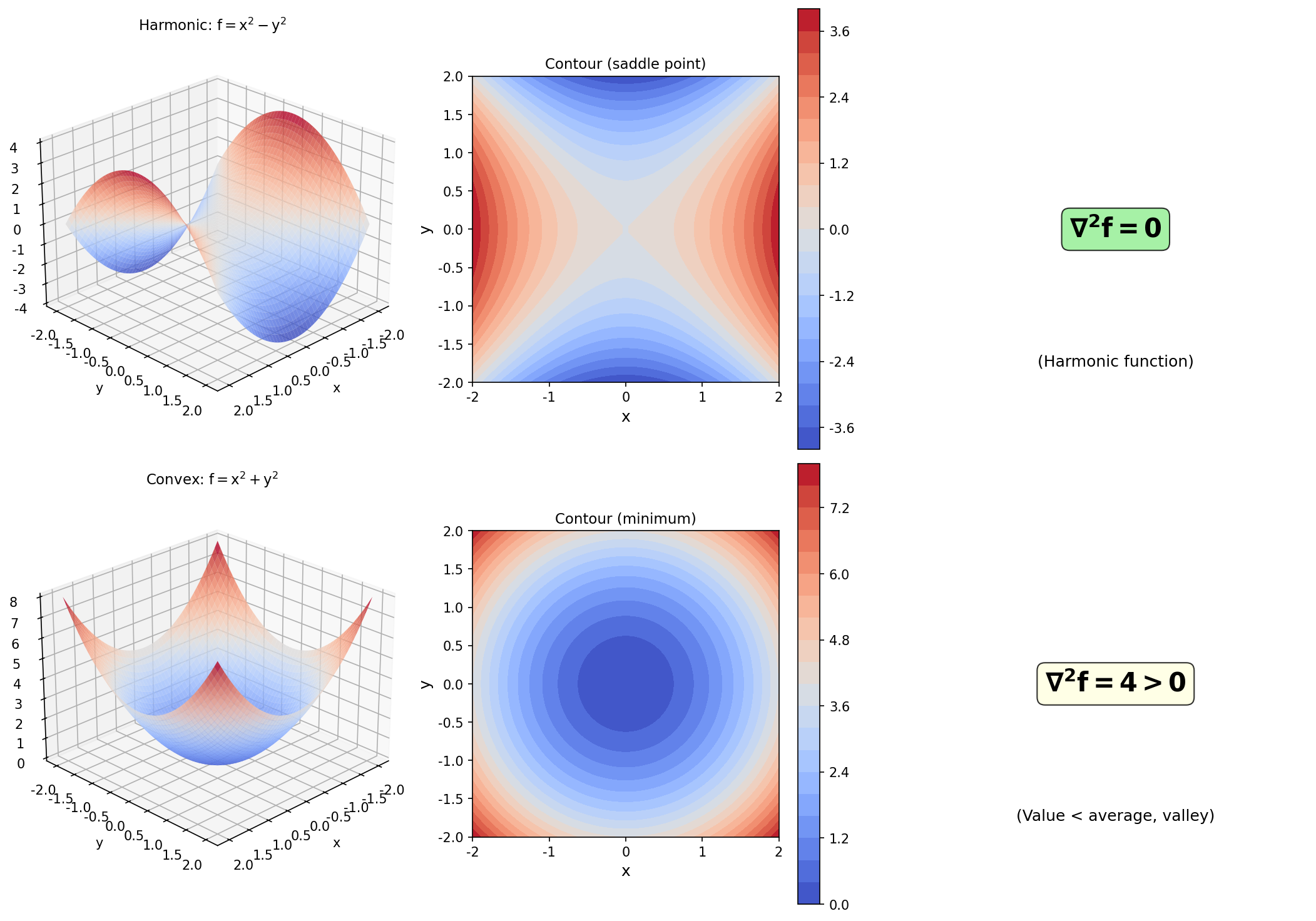
图6:二维拉普拉斯算子示例。上排:调和函数 $f=x^2-y^2$,$\nabla^2 f=0$(鞍点)。下排:凸函数 $f=x^2+y^2$,$\nabla^2 f=4>0$(极小值点)。
离散形式(五点格式):
$$[\nabla^2 f]{i,j} = \frac{f$$} + f_{i+1,j} + f_{i,j-1} + f_{i,j+1} - 4f_{i,j}}{h^2
模板表示:
$$\frac{1}{h^2} \begin{pmatrix} 0 & 1 & 0 \ 1 & -4 & 1 \ 0 & 1 & 0 \end{pmatrix}$$
三维情形
在三维中使用笛卡尔坐标 $(x, y, z)$:
$$\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}$$
数值示例:
- $f(x, y, z) = x^2 + y^2 + z^2$:$\nabla^2 f = 2 + 2 + 2 = 6 > 0$
- $f(x, y, z) = \frac{1}{r} = \frac{1}{\sqrt{x^2+y^2+z^2}}$:$\nabla^2 f = 0$($r > 0$,库仑势)
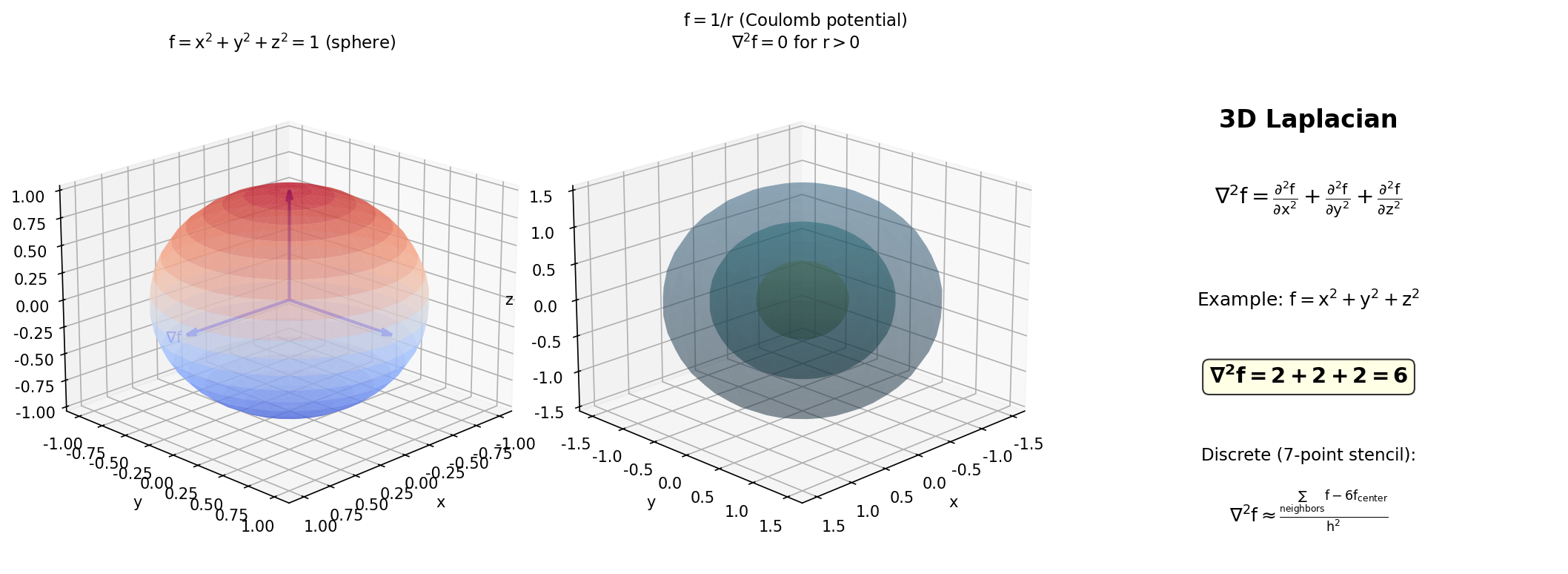
图7:三维拉普拉斯算子示例。左图:$f=x^2+y^2+z^2$ 的等值面(球面),梯度向外。中图:库仑势 $f=1/r$ 的等值面,$\nabla^2 f=0$。
三维拉普拉斯公式汇总:
$$\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}$$
具体计算示例:设 $f = x^2 + y^2 + z^2$
$$\frac{\partial^2 f}{\partial x^2} = 2, \quad \frac{\partial^2 f}{\partial y^2} = 2, \quad \frac{\partial^2 f}{\partial z^2} = 2$$
$$\nabla^2 f = 2 + 2 + 2 = 6$$
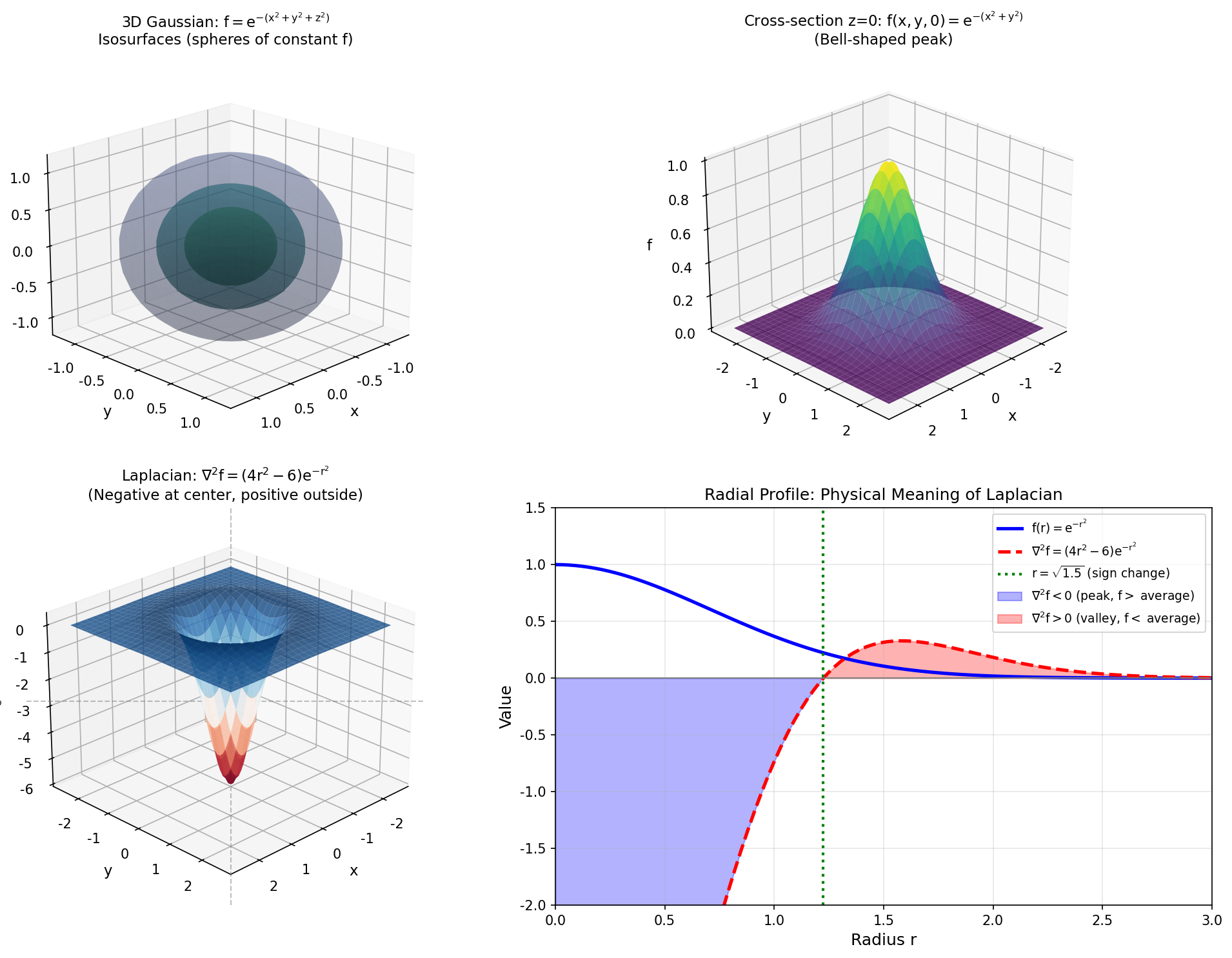
图8:三维拉普拉斯算子的连续形式与离散七点格式的可视化对比。
离散形式(七点格式):
$$[\nabla^2 f]{i,j,k} = \frac{f$$} + f_{i+1,j,k} + f_{i,j-1,k} + f_{i,j+1,k} + f_{i,j,k-1} + f_{i,j,k+1} - 6f_{i,j,k}}{h^2

图9:离散拉普拉斯算子模板。左:一维三点格式。中:二维五点格式(蓝色为正权重,红色为负权重)。右:二维九点格式(更高精度)。
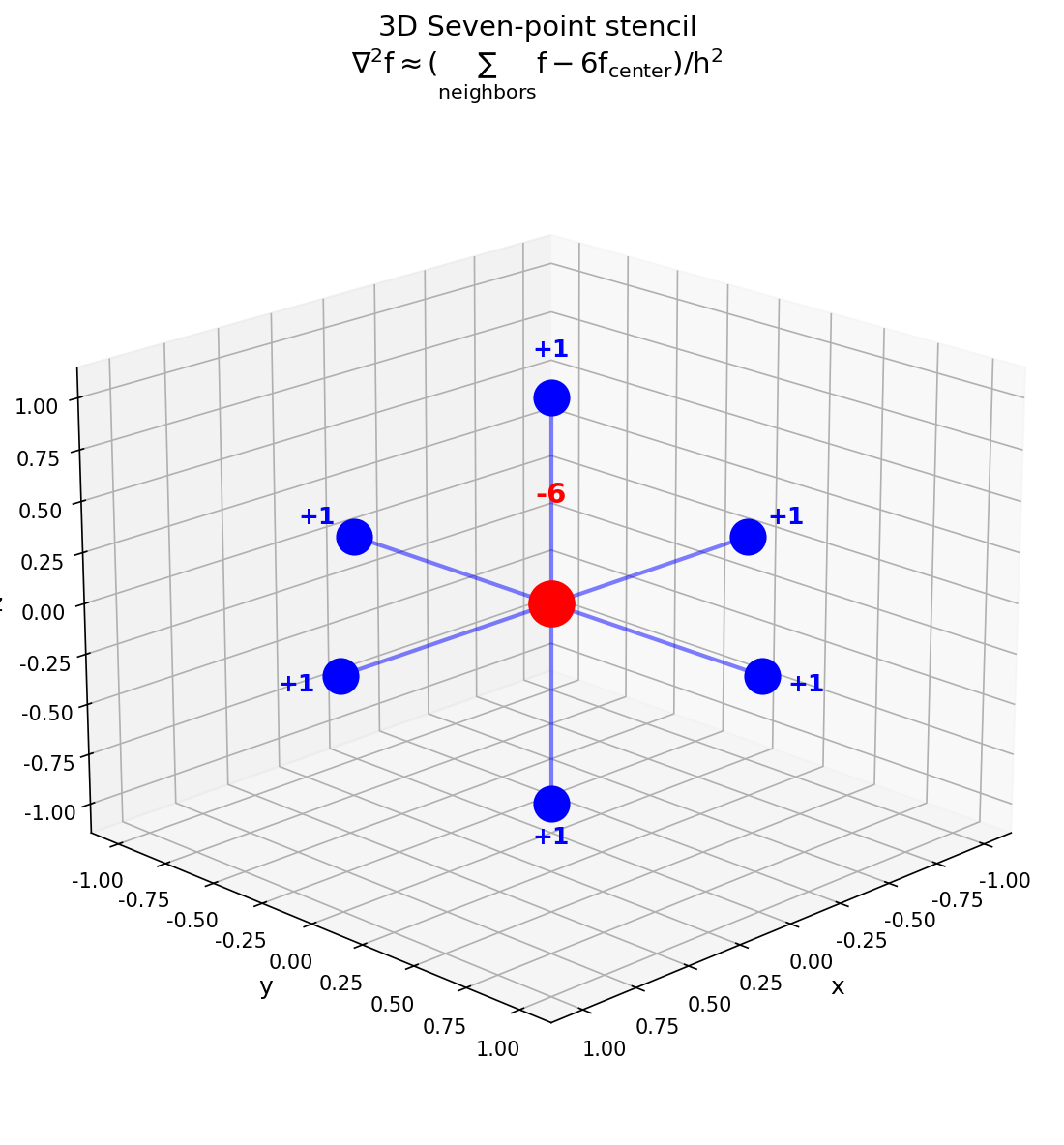
图10:三维七点格式模板。中心点权重为-6(红色),六个邻点权重为+1(蓝色),分别沿x、y、z三个坐标轴方向。
各维数拉普拉斯算子汇总
下面把常见维数下的连续形式与离散格式并列,便于横向对比。
| 维数 | 连续形式 | 离散格式(单位网格) |
|---|---|---|
| 1D | $\frac{d^2 f}{dx^2}$ | $f_{i-1} - 2f_i + f_{i+1}$ |
| 2D | $\frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$ | $f_{i-1,j} + f_{i+1,j} + f_{i,j-1} + f_{i,j+1} - 4f_{i,j}$ |
| 3D | $\sum_{k=1}^{3} \frac{\partial^2 f}{\partial x_k^2}$ | $\sum_{\text{邻点}} f - 6f_{\text{中心}}$ |
| nD | $\sum_{k=1}^{n} \frac{\partial^2 f}{\partial x_k^2}$ | $\sum_{\text{邻点}} f - 2n f_{\text{中心}}$ |
 CycleUser
CycleUser