CycleUser

本系列受到 Allen B. Downey 的《Modeling and Simulation in Python》的启发，旨在通过 Python 编程语言，帮助新手同学来探索数学建模的基础内容。

知识背景

在研究传染病传播或森林火灾等复杂系统时，数学家们通常使用两种主要的方法：

基于微分方程的方法（ODE） ：常微分方程（Ordinary Differential Equations）模型假设系统是均匀混合的。例如，它假设在一个城市中，任何一个人接触到感染者的概率都是一样的。这种方法擅长描述系统的宏观趋势（如感染总人数随时间的变化），但忽略了空间分布的细节。
基于元胞自动机的方法（CA） ：元胞自动机（Cellular Automata）引入了空间结构。它将世界划分为网格，每个网格（元胞）的状态只受其周围邻居的影响。这种方法能模拟出局部互动如何涌现出全局的复杂模式。

本章我们将通过两个经典案例——空间 SIR 模型和森林火灾模型，来深入探索基于元胞自动机的建模方法。

案例一：经典 SIR 模型 (ODE)

1. 概念介绍

SIR 模型是流行病学中最基础的模型，它将人群分为三类： * S (Susceptible) ：易感者。未得病，但缺乏免疫力，接触感染者后可能被传染。 * I (Infectious) ：感染者。已得病，并具有传染性。 * R (Recovered) ：康复者。已痊愈并获得免疫力（或死亡），不再参与传播。

2. 微分方程（“公式”）

在 ODE 模型中，我们假设人群是均匀混合的。模型的演化由以下三个微分方程描述：

易感者减少 ：易感者接触到感染者后被传染。 $$\frac{dS}{dt} = -\frac{\beta S I}{N}$$ 其中 $\beta$ 是传染率，$N$ 是总人口。
感染者变化 ：新增感染者减去康复者。 $$\frac{dI}{dt} = \frac{\beta S I}{N} - \gamma I$$ 其中 $\gamma$ 是康复率。
康复者增加 ：感染者康复。 $$\frac{dR}{dt} = \gamma I$$

这里有一个关键参数 基本传染数 $R_0 = \beta / \gamma$。如果 $R_0 > 1$，疫情将会爆发；如果 $R_0 < 1$，疫情会自然消亡。

3. 代码实现

我们使用 Python 的 scipy.integrate.odeint 来求解这些方程。完整代码请参考 code/04_sir_ode.py。

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# 1. 定义微分方程组
def sir_model(y, t, N, beta, gamma):
    S, I, R = y
    dSdt = -beta * S * I / N
    dIdt = beta * S * I / N - gamma * I
    dRdt = gamma * I
    return [dSdt, dIdt, dRdt]

# 2. 参数设置
N = 1000             # 总人口
beta = 0.3           # 传染率
gamma = 0.1          # 康复率 (平均康复期 10 天)
t = np.linspace(0, 160, 160)

# 3. 求解方程
y0 = [N-1, 1, 0]     # 初始状态: 999个易感者, 1个感染者
ret = odeint(sir_model, y0, t, args=(N, beta, gamma))
S, I, R = ret.T

# 4. 可视化
plt.plot(t, S/N, 'b', label='Susceptible')
plt.plot(t, I/N, 'r', label='Infected')
plt.plot(t, R/N, 'g', label='Recovered')
plt.legend()
plt.show()

4. 可视化结果

运行上述代码，我们会得到经典的 SIR 曲线：

红色曲线 (I) ：感染人数先指数级上升，达到峰值后缓慢下降。
蓝色曲线 (S) ：易感人数单调下降，最终稳定在一个非零值（并未全员感染）。
绿色曲线 (R) ：康复人数单调上升。

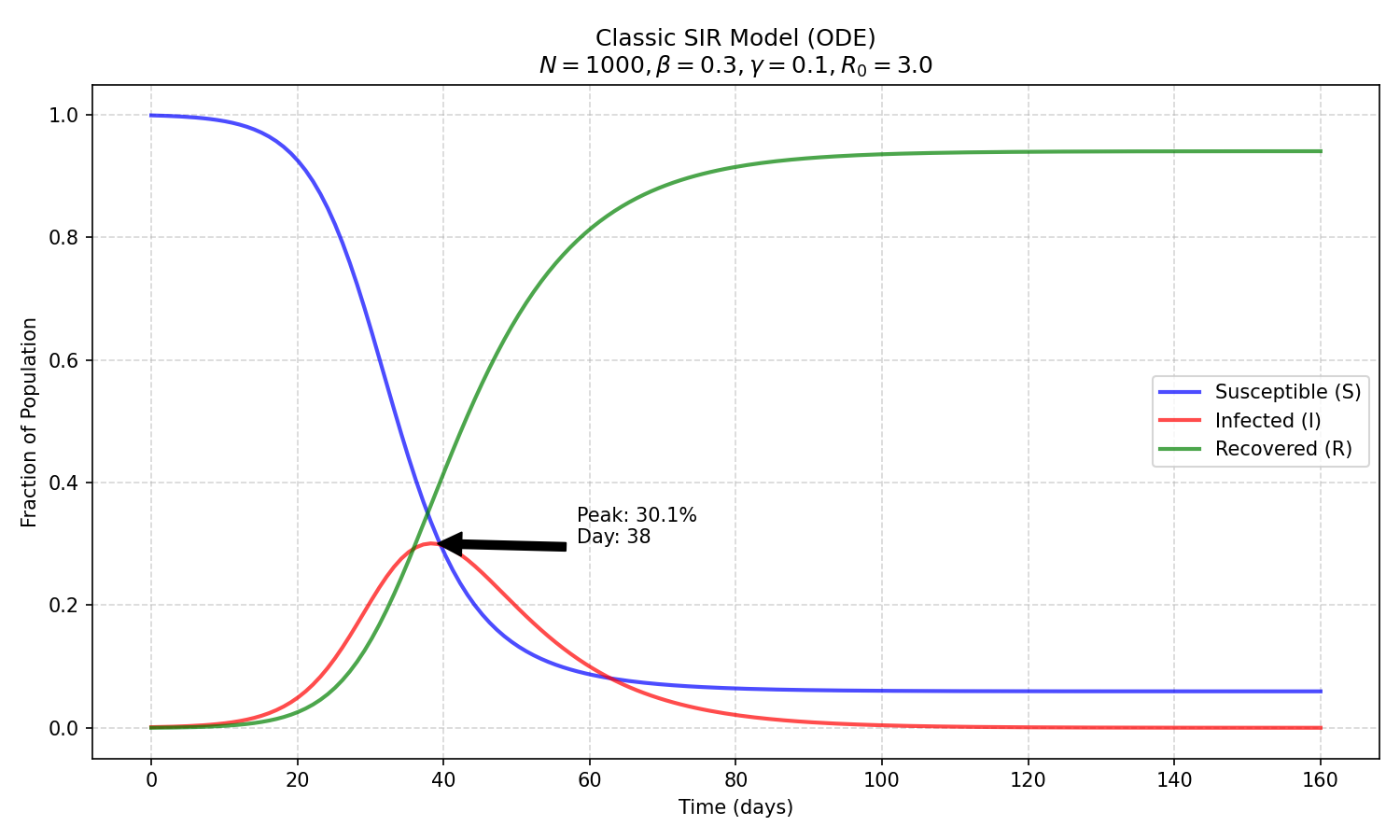
Classic SIR Model

这种模型非常适合预测疫情的大趋势，比如“何时达到峰值”或“最终会有多少人感染”。但它无法告诉我们疫情在城市中具体的传播路径。

元胞自动机 (Cellular Automata)？

在深入空间模型之前，我们需要先了解一下它们的数学基础——元胞自动机 (CA)。

1. 核心概念

想象一个巨大的棋盘。棋盘上的每一个格子，我们称之为元胞 (Cell)。元胞自动机不是一台机器，而是一个数学模型，它由以下几个部分组成：

网格 (Lattice) ：所有元胞排列成一个规则的空间，通常是一维的线、二维的平面（像棋盘）或三维的立体。
状态 (State) ：每个元胞在任何时刻都有一个特定的状态。比如在生命游戏中，状态只有“生”和“死”；在红绿灯模型中，状态可能是“红”、“黄”、“绿”。
邻居 (Neighborhood) ：一个元胞的“朋友圈”。它决定了谁能影响这个元胞。最常见的有两种：
- 冯·诺依曼邻居 (Von Neumann) ：只有上、下、左、右 4 个邻居。
- 摩尔邻居 (Moore) ：包括对角线方向的 8 个邻居（就像扫雷游戏里的九宫格）。
规则 (Rule) ：这是 CA 的灵魂。规则决定了下一时刻元胞的状态如何变化。最关键的是，规则是局部的（Local）——一个元胞下一刻变成什么样，只取决于它自己和它邻居当前的状态，与远处发生了什么无关。

2. 涌现 (Emergence)

元胞自动机最迷人的地方在于：虽然每个元胞都只遵循极其简单的局部规则（比如“邻居着火我就着火”），但当成千上万个元胞聚在一起时，整个系统会表现出极其复杂、甚至看似有智能的宏观行为（比如形成美丽的波纹、分形图案，甚至模拟生命活动）。

这种“由简入繁”的现象，被称为涌现。它是复杂系统理论的核心，解释了为什么简单的原子能组成复杂的生命，简单的神经元能产生复杂的意识。

案例二：空间 SIR 模型 (Spatial SIR Model)

1. 概念介绍

为了弥补 ODE 模型忽略空间结构的缺陷，我们引入元胞自动机。在空间模型中，我们依然使用 S、I、R 三种状态，但引入了Moore 邻域（Moore Neighborhood）的概念。

对于网格上的任意一个点，它的邻居是指周围一圈的 8 个格子（上、下、左、右、左上、右上、左下、右下）。

2. 演化规则（“公式”）

不同于微分方程使用连续的时间和变量，元胞自动机使用离散的时间步和状态。其核心演化规则如下：

传染规则 ($S \to I$) ：如果一个元胞的状态是 $S$（易感），且其 8 个邻居中至少有一个是 $I$（感染），那么在下一个时间步，它有 $\beta$ 的概率变成 $I$。 $$P(S_{t+1}=I | S_t) = 1 - (1-\beta)^{k}$$ (注：$k$ 是邻居中感染者的数量。在简化代码中，我们通常对每个感染邻居独立判定)
康复规则 ($I \to R$) ：如果一个元胞的状态是 $I$（感染），在下一个时间步，它有 $\gamma$ 的概率变成 $R$（康复）。这模拟了病程的持续时间。
免疫规则 ($R \to R$) ：一旦变成 $R$，状态将不再改变（获得永久免疫）。

3. 代码实现

我们使用 Python 的 numpy 库来处理网格运算。完整代码如下：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.colors import ListedColormap

# 设置随机种子
np.random.seed(42)

# ==========================================
# SIR 模型参数设置
# ==========================================
GRID_SIZE = 100        # 网格大小 100x100
BETA = 0.3             # 传染率 (S -> I)
GAMMA = 0.1            # 康复率 (I -> R)
INIT_INFECTED = 0.005  # 初始感染比例

# 状态定义
SUSCEPTIBLE = 0  # 易感者 (S) - 绿色
INFECTED = 1     # 感染者 (I) - 红色
RECOVERED = 2    # 康复者 (R) - 灰色

# 初始化网格
grid = np.zeros((GRID_SIZE, GRID_SIZE), dtype=int)
# 随机选择初始感染者
infected_indices = np.random.choice(
    GRID_SIZE * GRID_SIZE, 
    int(GRID_SIZE * GRID_SIZE * INIT_INFECTED), 
    replace=False
)
grid.flat[infected_indices] = INFECTED

# 定义邻居偏移量 (Moore 邻域：8个邻居)
neighbors = [(-1, -1), (-1, 0), (-1, 1),
             (0, -1),           (0, 1),
             (1, -1),  (1, 0),  (1, 1)]

def update_sir(frame):
    global grid
    new_grid = grid.copy()

    # 获取所有感染者的坐标
    infected_rows, infected_cols = np.where(grid == INFECTED)

    # 1. 传染过程 (I -> S)
    for r, c in zip(infected_rows, infected_cols):
        # 尝试传染周围 8 个邻居
        for dr, dc in neighbors:
            nr, nc = r + dr, c + dc
            # 边界检查
            if 0 <= nr < GRID_SIZE and 0 <= nc < GRID_SIZE:
                if grid[nr, nc] == SUSCEPTIBLE:
                    if np.random.random() < BETA:
                        new_grid[nr, nc] = INFECTED

    # 2. 康复过程 (I -> R)
    # 每个感染者有概率 GAMMA 康复
    recover_mask = (grid == INFECTED) & (np.random.random((GRID_SIZE, GRID_SIZE)) < GAMMA)
    new_grid[recover_mask] = RECOVERED

    grid = new_grid
    mat.set_data(grid)
    return [mat]

# ==========================================
# 可视化设置
# ==========================================
fig, ax = plt.subplots(figsize=(6, 6))
# 自定义颜色映射：0-绿色，1-红色，2-灰色
cmap = ListedColormap(['#2ecc71', '#e74c3c', '#95a5a6'])
mat = ax.matshow(grid, cmap=cmap, vmin=0, vmax=2)

ax.set_axis_off()
ax.set_title(f'Spatial SIR Model\nBeta={BETA}, Gamma={GAMMA}', fontsize=14)

# 添加图例
from matplotlib.patches import Patch
legend_elements = [
    Patch(facecolor='#2ecc71', label='Susceptible'),
    Patch(facecolor='#e74c3c', label='Infected'),
    Patch(facecolor='#95a5a6', label='Recovered')
]
ax.legend(handles=legend_elements, loc='upper right', bbox_to_anchor=(1.1, 1.1))

plt.tight_layout()

# 生成动画
ani = FuncAnimation(fig, update_sir, frames=200, interval=50, blit=True)
ani.save('../images/04_sir_spatial.gif', writer='pillow', fps=15)
plt.close(fig)
print("SIR animation saved to ../images/04_sir_spatial.gif")

4. 可视化结果

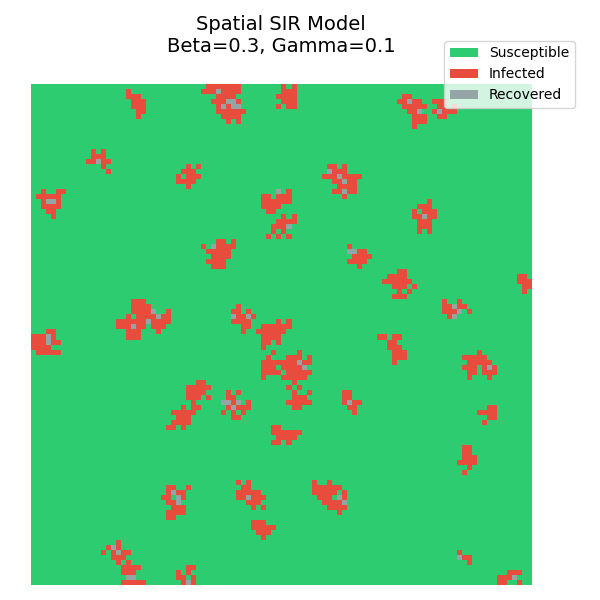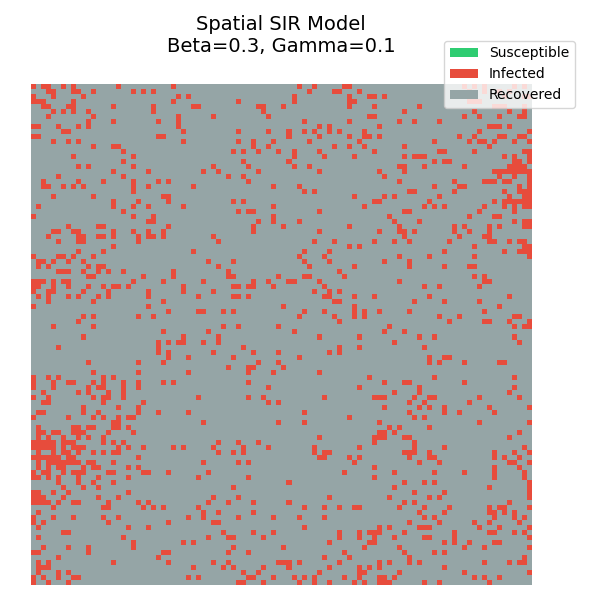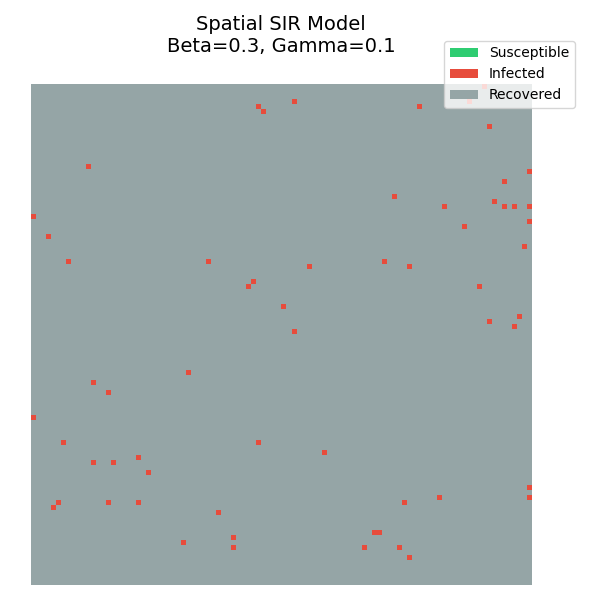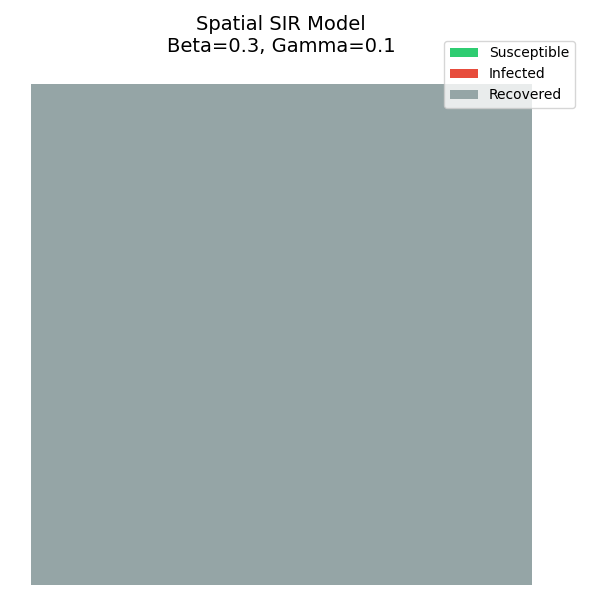
运行模拟，你会看到疫情像波浪一样从感染中心向外扩散。

波状扩散 ：不同于均匀混合模型的指数爆炸，空间限制使得疫情只能一层层向外推移。
免疫屏障 ：随着康复者（灰色）的增加，它们像一堵墙一样阻断了传播路径，保护了剩余的易感者。

Spatial SIR Simulation

案例三：森林火灾模型 (Forest Fire Model)

1. 概念介绍

森林火灾模型是复杂系统理论中用于展示自组织临界性（Self-Organized Criticality, SOC）的经典模型。

在这个模型中，网格上的每个点有三种可能的状态： * 空地 (Empty) ：黑色。 * 树木 (Tree) ：绿色。 * 燃烧 (Burning) ：红色。

2. 演化规则

我们采用著名的 Drossel-Schwabl 模型规则，系统按照以下顺序循环演化：

燃烧蔓延规则 ：如果一棵树（Tree）的 8 个邻居中至少有一个在燃烧（Burning），这棵树将在下一时刻变成燃烧状态。 $$\text{Tree} \xrightarrow{\exists \text{Neighbor} = \text{Burning}} \text{Burning}$$
熄灭规则 ：正在燃烧的树（Burning）在下一时刻变成空地（Empty）。 $$\text{Burning} \to \text{Empty}$$
生长规则 ：一块空地（Empty）以极小的概率 $p$ 长出新树（Tree）。这是系统积累能量的过程。 $$\text{Empty} \xrightarrow{p} \text{Tree}$$
闪电规则 ：一棵树（Tree）即便没有邻居燃烧，也有极极小的概率 $f$ 被闪电击中而燃烧。这是触发雪崩的扰动。 $$\text{Tree} \xrightarrow{f} \text{Burning}$$

通常设置 $f \ll p$，意味着树木生长相对较快，而闪电极少发生。

3. 代码实现

完整代码如下：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.colors import ListedColormap

# 设置随机种子
np.random.seed(42)

# ==========================================
# 森林火灾模型参数设置
# ==========================================
GRID_SIZE = 128        # 网格大小
GROWTH_PROB = 0.01     # 树木生长概率 (P)
FIRE_PROB = 0.0001     # 闪电起火概率 (F)

# 状态定义
EMPTY = 0    # 空地 (黑色)
TREE = 1     # 树木 (绿色)
BURNING = 2  # 燃烧 (红色)

# 初始化网格
grid = np.random.choice([EMPTY, TREE], size=(GRID_SIZE, GRID_SIZE), p=[0.5, 0.5])

# 定义邻居偏移量 (Moore 邻域：8个邻居)
neighbors = [(-1, -1), (-1, 0), (-1, 1),
             (0, -1),           (0, 1),
             (1, -1),  (1, 0),  (1, 1)]

def update_forest(frame):
    global grid
    new_grid = grid.copy()

    # 规则 1: 燃烧的树变成空地 (Burning -> Empty)
    burning_indices = np.where(grid == BURNING)
    new_grid[burning_indices] = EMPTY

    # 规则 2: 树木如果邻居有火，则燃烧 (Tree -> Burning)
    # 或者如果被闪电击中，则燃烧 (Tree -> Burning)
    tree_indices = np.where(grid == TREE)

    # 检查邻居是否有火
    for r, c in zip(*tree_indices):
        has_fire_neighbor = False
        for dr, dc in neighbors:
            nr, nc = r + dr, c + dc
            if 0 <= nr < GRID_SIZE and 0 <= nc < GRID_SIZE:
                if grid[nr, nc] == BURNING:
                    has_fire_neighbor = True
                    break

        if has_fire_neighbor:
            new_grid[r, c] = BURNING
        elif np.random.random() < FIRE_PROB: # 闪电起火
            new_grid[r, c] = BURNING

    # 规则 3: 空地有概率长出新树 (Empty -> Tree)
    empty_indices = np.where(grid == EMPTY)
    growth_mask = np.random.random(len(empty_indices[0])) < GROWTH_PROB
    new_grid[empty_indices[0][growth_mask], empty_indices[1][growth_mask]] = TREE

    grid = new_grid
    mat.set_data(grid)
    return [mat]

# ==========================================
# 可视化设置
# ==========================================
fig, ax = plt.subplots(figsize=(6, 6))
# 自定义颜色映射：0-黑色，1-绿色，2-红色
cmap = ListedColormap(['black', '#2ecc71', '#e74c3c'])
mat = ax.matshow(grid, cmap=cmap, vmin=0, vmax=2)

ax.set_axis_off()
ax.set_title(f'Forest Fire Simulation\nGrowth P={GROWTH_PROB}, Lightning F={FIRE_PROB}', fontsize=14)

# 添加图例
from matplotlib.patches import Patch
legend_elements = [
    Patch(facecolor='black', label='Empty'),
    Patch(facecolor='#2ecc71', label='Tree'),
    Patch(facecolor='#e74c3c', label='Burning')
]
ax.legend(handles=legend_elements, loc='upper right', bbox_to_anchor=(1.1, 1.1))

plt.tight_layout()

# 生成动画
ani = FuncAnimation(fig, update_forest, frames=200, interval=50, blit=True)
ani.save('../images/04_forest_fire.gif', writer='pillow', fps=15)
plt.close(fig)
print("Forest fire animation saved to ../images/04_forest_fire.gif")

4. 可视化结果与自组织临界性

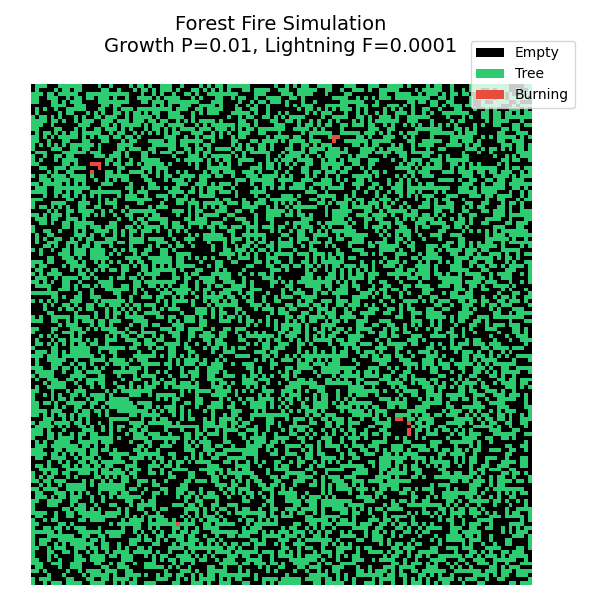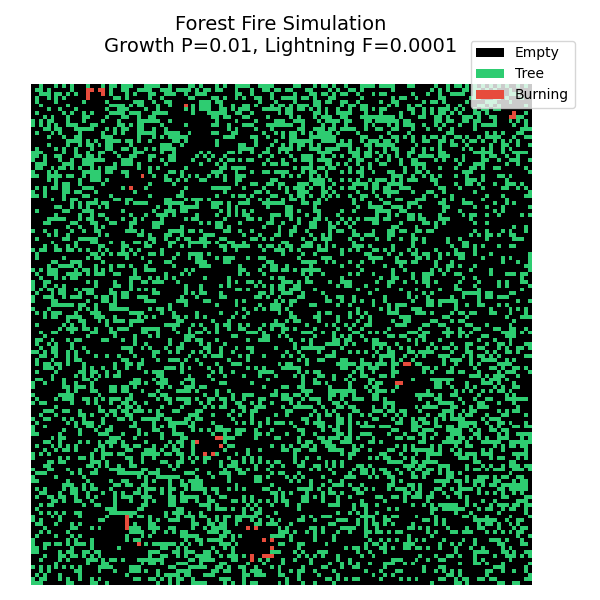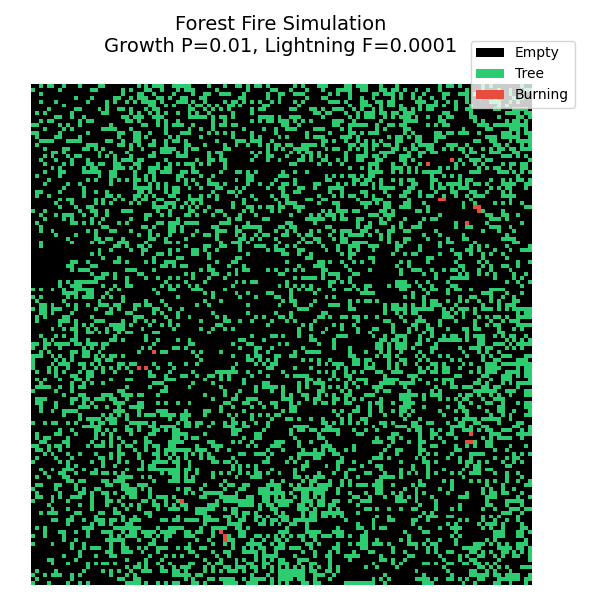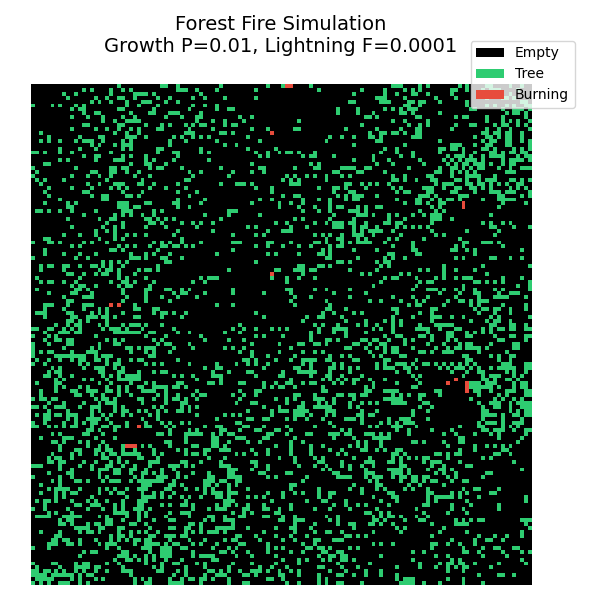
Forest Fire Simulation

在这个模拟中，我们可以观察到一种迷人的动态平衡：

积累阶段 ：树木慢慢生长，森林变得越来越茂密。这时候如果有闪电，火势也烧不起来，因为树与树之间是不连通的。
临界状态 ：当树木密度达到某个临界值时，森林形成了一个巨大的连通网络。
释放阶段（雪崩） ：此时，一道微小的闪电就能引燃整个网络，造成一场覆盖全图的超级大火。
循环：大火过后，留下一片空地，循环重新开始。

自组织临界性 (SOC) 指的就是这种现象：系统不需要外部的精细调节，会自动演化并停留在“临界点”附近。在这个状态下，任何规模的事件（从烧毁一棵树到烧毁整个森林）都有可能发生，且事件规模遵循幂律分布。这解释了为什么自然界中地震、山崩等灾难难以预测——因为它们是系统内在动力学的必然产物。

总结

通过本章的两个模型，我们不仅学习了如何使用 Python 的元胞自动机来模拟空间传播过程，还深入理解了空间结构对系统行为的决定性影响。从传染病的波状扩散到森林火灾的周期性爆发，这些复杂的宏观现象都源于简单的微观局部规则。