本系列受到 Allen B. Downey 的《Modeling and Simulation in Python》的启发,旨在通过 Python 编程语言,帮助新手同学来探索数学建模的基础内容。
知识背景
你可能听说过这样一个都市传说:如果有人从帝国大厦的顶楼扔下一枚硬币,这枚硬币在落地时会因为速度太快,嵌入水泥地面,甚至击穿行人的头骨。
这个传说听起来很吓人,但它是真的吗?
为了验证这个说法,我们可以使用建模(Modeling)的方法。建模就是把复杂的现实世界简化,只保留最核心的要素,然后通过数学公式或计算机模拟来预测结果。在本篇文章中,我们将通过两个不同复杂度的物理模型,来揭开这个流言的真相。
概念介绍
在开始计算之前,我们需要了解几个核心概念:
- 抽象(Abstraction):决定在模型中保留什么,忽略什么。例如,我们可能暂时忽略风速、空气湿度或硬币的旋转,只关注重力和空气阻力。
- 迭代建模(Iterative Modeling):从最简单的模型开始,逐步增加细节。如果简单模型就能说明问题,就不需要复杂的;如果不够,再一点点加。
- 单位运算:在科学计算中,数字必须带有单位(如米、秒)才有意义。Python 中的
Pint库可以帮我们自动处理单位换算,避免“火星气候探测者号”坠毁那样的悲剧。
公式推导
我们首先建立一个最简单的模型:假设没有空气阻力,硬币只受重力影响。
在这个模型中,硬币做自由落体运动。 设重力加速度为 $a$(约 $9.8 \text{ m/s}^2$),下落时间为 $t$。
速度 $v$ 随时间变化的公式是: $$ v = a t $$
下落距离 $x$ 的公式是: $$ x = \frac{1}{2} a t^2 $$
如果我们知道帝国大厦的高度 $h$(约 $381$ 米),我们可以反推落地所需的时间 $t$: $$ t = \sqrt{\frac{2h}{a}} $$
然后将这个时间代入速度公式,就能算出落地时的速度。
代码实现
我们使用 Python 来进行计算。为了确保严谨,我们会使用 Pint 库来管理单位。
1. 准备工作
首先导入必要的库。
from numpy import sqrt
from pint import UnitRegistry
# 创建单位注册表
units = UnitRegistry()
# 定义基本单位
meter = units.meter
second = units.second
2. 模型一:忽略空气阻力
让我们看看在真空环境下,硬币会有多快。
# 定义参数
a = 9.8 * meter / second**2 # 重力加速度
h = 381 * meter # 帝国大厦高度
# 计算落地时间
t = sqrt(2 * h / a)
print(f"落地时间: {t:.2f}")
# 计算落地速度
v = a * t
print(f"落地速度: {v:.2f}")
运行结果显示,落地速度约为 86 m/s。 这是什么概念呢?我们把它换算成更熟悉的“英里每小时”(mph):
mile = units.mile
hour = units.hour
v_mph = v.to(mile/hour)
print(f"时速: {v_mph:.2f}")
结果大约是 190 mph(约 300 公里/小时)。这简直就是一颗子弹!如果这个模型是正确的,那么硬币确实能杀人。
3. 模型二:考虑空气阻力
但是,我们忽略了一个至关重要的因素:空气。 在现实中,物体下落时会受到空气阻力。速度越快,阻力越大。当阻力等于重力时,物体就不再加速,而是以终端速度(Terminal Velocity)匀速下落。
对于一枚硬币,由于它扁平且轻,受空气阻力影响非常大。实际上,硬币的终端速度只有约 29 m/s(约 65 mph)。
让我们用这个更接近现实的数据重新评估:
v_terminal = 29 * meter / second
v_terminal_mph = v_terminal.to(mile/hour)
print(f"实际落地时速: {v_terminal_mph:.2f}")
结果只有 65 mph(约 100 公里/小时)。虽然被砸到肯定会很痛,可能会起个大包,但绝不可能击穿头骨,更不可能嵌入水泥地。
可视化展示
虽然本章主要是代数计算,但我们可以通过一个炫酷的动态对比图来直观感受两个模型的差异。
1. 完整代码
我们使用 matplotlib.animation 来制作一个动态 GIF。这个动画不仅模拟了硬币的下落过程,还通过镜头跟随和实时仪表盘,让你仿佛置身于帝国大厦的实验现场。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import matplotlib.patches as patches
# ==========================================
# 物理模型参数
# ==========================================
H = 381.0 # 帝国大厦高度 (m)
g = 9.8 # 重力加速度 (m/s^2)
v_term = 29.0 # 终端速度 (m/s)
# 时间设置
dt = 0.1
t_max = 15.0 # 模拟时长
steps = int(t_max / dt)
time = np.linspace(0, t_max, steps)
# 1. 真空模型 (Vacuum Model)
y_vac = H - 0.5 * g * time**2
v_vac = g * time
# 落地修正
mask_vac = y_vac < 0
y_vac[mask_vac] = 0
v_vac[mask_vac] = 0
# 2. 空气阻力模型 (Air Resistance Model)
# 简化模拟:先加速到终端速度,然后匀速
# 达到终端速度的时间
t_term = v_term / g
y_air = np.zeros_like(time)
v_air = np.zeros_like(time)
for i, t in enumerate(time):
if t < t_term:
# 加速阶段
v_air[i] = g * t
y_air[i] = H - 0.5 * g * t**2
else:
# 匀速阶段
v_air[i] = v_term
# y = y_at_term - v_term * (t - t_term)
y_at_term = H - 0.5 * g * t_term**2
y_air[i] = y_at_term - v_term * (t - t_term)
# 落地修正
if y_air[i] < 0:
y_air[i] = 0
v_air[i] = 0
# ==========================================
# 炫酷可视化设置
# ==========================================
plt.style.use('dark_background')
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6), gridspec_kw={'width_ratios': [1, 1.5]})
# --- 左图:大楼全景视角 (Empire State Building View) ---
ax1.set_xlim(-10, 20)
ax1.set_ylim(0, 420)
ax1.set_title("Empire State Drop Test", color='white', fontsize=14, pad=20)
ax1.set_ylabel("Height (m)")
# 绘制大楼轮廓
building = patches.Rectangle((-5, 0), 10, 381, linewidth=2, edgecolor='#3498db', facecolor='#2c3e50', alpha=0.5)
ax1.add_patch(building)
# 地面
ground = ax1.axhline(0, color='#2ecc71', lw=3)
ax1.text(-8, 5, 'Ground', color='#2ecc71', fontsize=10)
# 硬币对象
coin_vac, = ax1.plot([], [], 'o', color='#e74c3c', markersize=8, label='Vacuum Model') # 红色
coin_air, = ax1.plot([], [], 'o', color='#f1c40f', markersize=8, label='Real Model') # 黄色
# 轨迹线
trail_vac, = ax1.plot([], [], '--', color='#e74c3c', alpha=0.5, lw=1)
trail_air, = ax1.plot([], [], '-', color='#f1c40f', alpha=0.5, lw=1)
ax1.legend(loc='upper right', frameon=False)
# --- 右图:速度仪表盘 & 冲击力模拟 (Dashboard View) ---
ax2.set_xlim(0, t_max)
ax2.set_ylim(0, 100)
ax2.set_title("Velocity & Impact Analysis", color='white', fontsize=14, pad=20)
ax2.set_xlabel("Time (s)")
ax2.set_ylabel("Velocity (m/s)")
ax2.grid(True, linestyle='--', alpha=0.3)
# 速度曲线
line_v_vac, = ax2.plot([], [], '--', color='#e74c3c', lw=2, label='Vacuum Velocity')
line_v_air, = ax2.plot([], [], '-', color='#f1c40f', lw=2, label='Real Velocity')
# 终端速度参考线
ax2.axhline(v_term, color='#f1c40f', linestyle=':', alpha=0.6)
ax2.text(0.5, v_term + 2, f'Terminal Velocity: {v_term} m/s', color='#f1c40f', fontsize=8)
# 实时数据文本
text_h = ax2.text(0.05, 0.9, '', transform=ax2.transAxes, color='white', fontsize=10)
text_v = ax2.text(0.05, 0.85, '', transform=ax2.transAxes, color='white', fontsize=10)
# 落地累积效果 (Impact Accumulation)
impact_scatter = ax1.scatter([], [], color='#ecf0f1', s=20, alpha=0.6, marker='x')
impact_points = []
# 镜头切换逻辑
# 0-5s: 全景; 5-10s: 追踪下落; 10s+: 落地特写
def update(frame):
current_time = time[frame]
# 1. 更新位置和速度
h_v = y_vac[frame]
h_a = y_air[frame]
vel_v = v_vac[frame]
vel_a = v_air[frame]
# 更新硬币
coin_vac.set_data([0], [h_v])
coin_air.set_data([5], [h_a])
# 更新轨迹
trail_vac.set_data([0]*frame, y_vac[:frame])
trail_air.set_data([5]*frame, y_air[:frame])
# 更新速度曲线
line_v_vac.set_data(time[:frame], v_vac[:frame])
line_v_air.set_data(time[:frame], v_air[:frame])
# 更新文本
text_h.set_text(f"Height: Vac={h_v:.1f}m | Real={h_a:.1f}m")
text_v.set_text(f"Speed: Vac={vel_v:.1f}m/s | Real={vel_a:.1f}m/s")
# 2. 镜头控制 (Camera Control)
if h_a > 100:
# 高空俯瞰
ax1.set_ylim(h_a - 200, h_a + 50)
elif h_a > 0:
# 接近地面
ax1.set_ylim(0, 200)
else:
# 落地后保持地面视角
ax1.set_ylim(0, 50)
# 3. 落地堆积效果
if frame % 5 == 0: # 模拟多次实验的累积
impact_points.append([np.random.normal(5, 1), 0])
if len(impact_points) > 0:
arr = np.array(impact_points)
impact_scatter.set_offsets(arr)
return coin_vac, coin_air, trail_vac, trail_air, line_v_vac, line_v_air, text_h, text_v, impact_scatter
# 生成动画
ani = FuncAnimation(fig, update, frames=steps, interval=30, blit=True)
ani.save('01_falling_penny_cool.gif', writer='pillow', fps=30)
plt.close(fig)
2. 动态演示效果
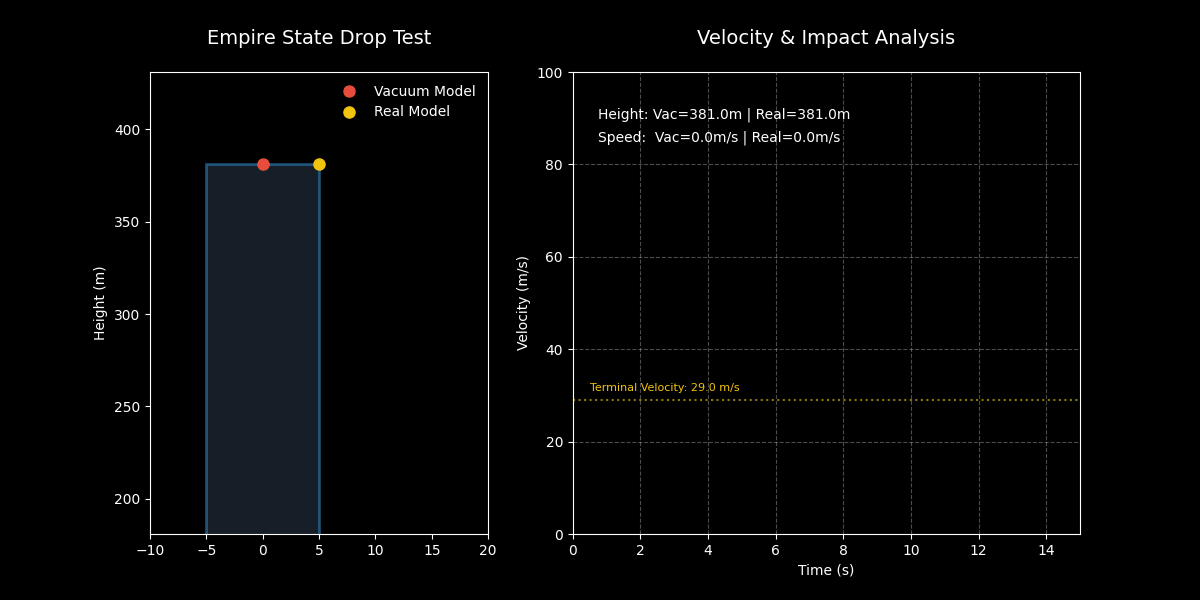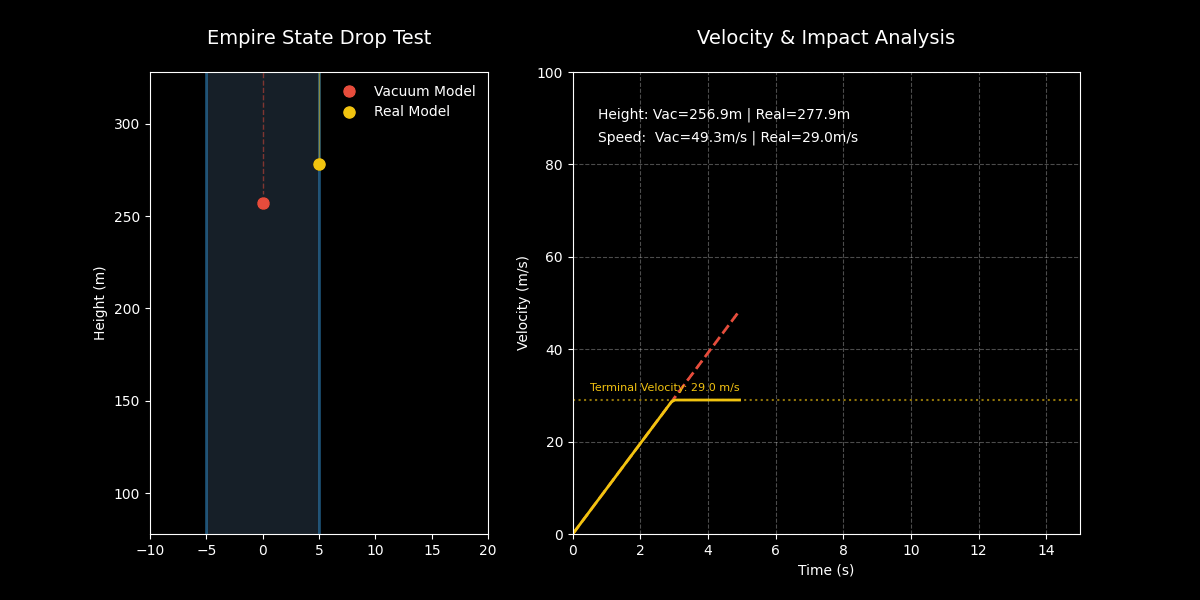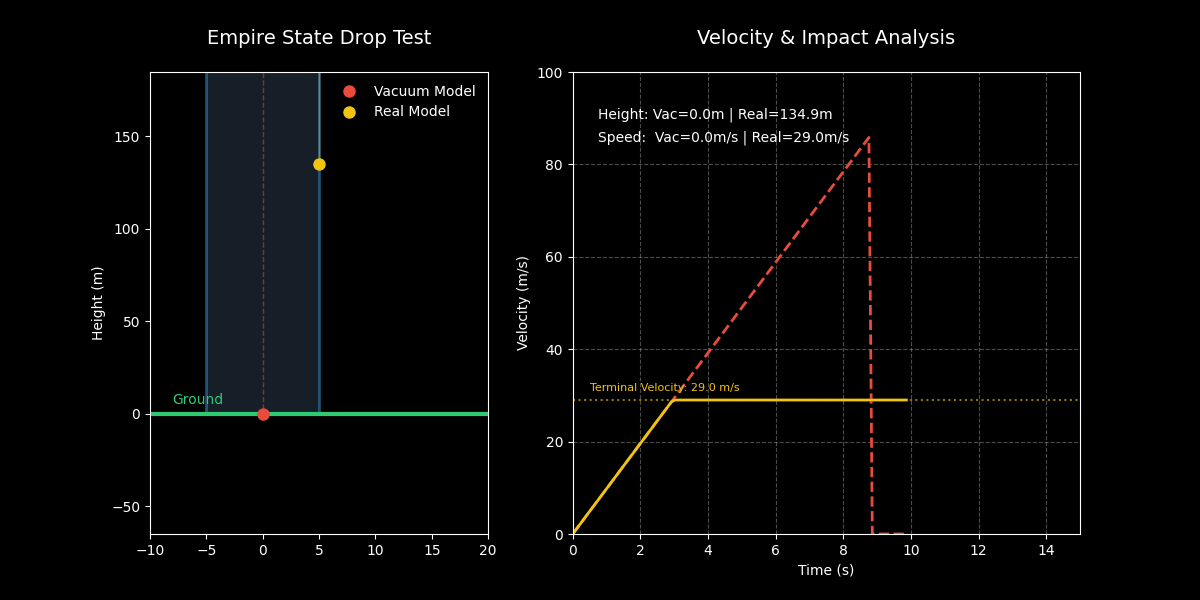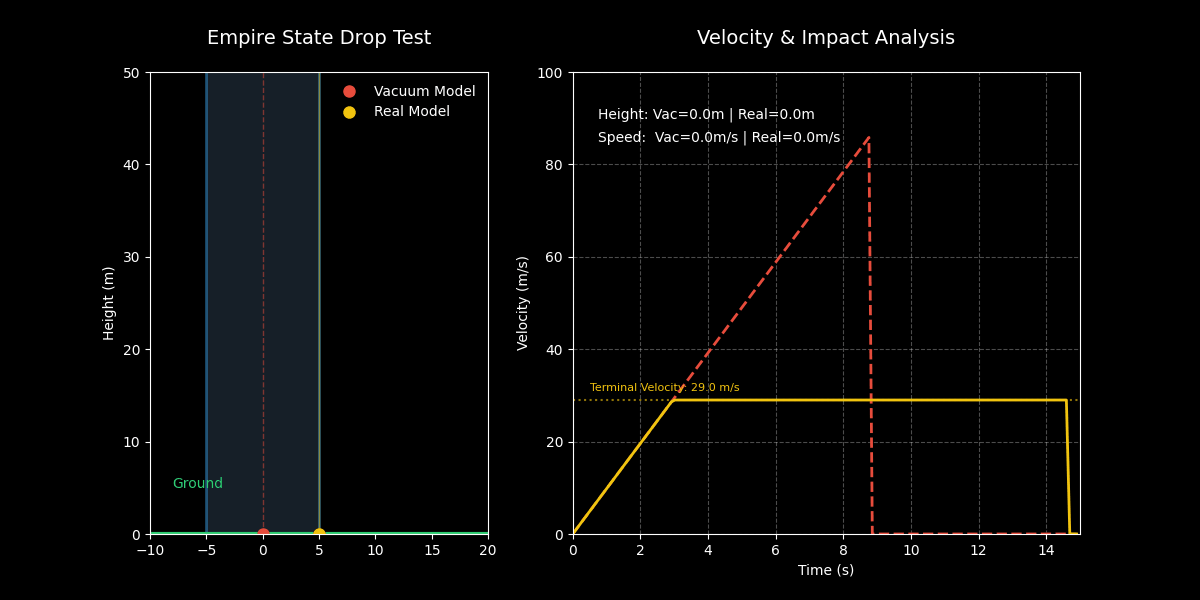
通过这个动画,我们可以清晰地观察到: 1. 初始阶段:两者几乎同步下落。 2. 加速阶段:真空模型(红色)持续加速,迅速超越现实模型(黄色)。 3. 终端速度:现实模型在大约 3 秒后达到终端速度(29 m/s),之后匀速下落。 4. 最终结果:真空中的硬币像子弹一样砸向地面,而现实中的硬币则缓缓飘落(相对而言),并没有传说中那么可怕。
总结
通过这个案例,我们学到了建模的核心思想: 1. 所有模型都是不准确的:模型一忽略了空气阻力,它是不准确的。模型二假设硬币瞬间达到终端速度,也是简化的,严格来说也是有误差的。 2. 但有些模型是有用的:模型二虽然简化,但它给出的结论(硬币砸不死人)与《流言终结者》的实验结果一致。这就足够解决我们的问题了。
这就是科学建模的魅力:我们不需要复刻整个宇宙,只需要捕捉到关键的相关规律。
 CycleUser
CycleUser