本系列受到 Allen B. Downey 的《Modeling and Simulation in Python》的启发,旨在通过 Python 编程语言,帮助新手同学来探索数学建模的基础内容。
知识背景
在开始探索如何用代码模拟现实世界之前,我们需要先了解几个核心概念。建模(Modeling) 是对现实系统的抽象和简化,目的是为了理解系统的运作机制或预测未来的行为。仿真(Simulation) 则是基于模型,通过计算机程序来模拟系统随时间演变的过程。
在本篇文章中,我们将使用 Python 语言来构建模型。如果你对 Python 的函数定义、条件判断(if)、循环(for)以及基本的变量操作有一定了解,那么你已经具备了阅读本文的基础。我们将从最简单的状态记录开始,一步步构建出一个能够评估共享单车系统服务质量的完整模型。
概念介绍
想象一下,有两个地点——校园(Campus)和地铁站(Metro Station),它们之间有一套共享单车系统。人们可以在一个地点借车,骑到另一个地点还车。
为了模拟这个系统,我们需要关注以下几个关键点: 1. 状态(State):系统在某一时刻的样子。这里主要指校园和地铁站当前停放的单车数量。 2. 时间步(Time Step):模拟时间的最小单位。我们可以假设每分钟是一个时间步。 3. 事件(Event):在每个时间步内可能发生的事情,比如有人从校园借车骑去地铁站。 4. 随机性(Randomness):现实中人流到达的时刻是不确定的,我们需要用概率来模拟这种随机性。 5. 度量指标(Metrics):用来评价系统好坏的标准,例如有多少人因为没车而无法出行(不满意的客户)。
模型构建与代码实现
1. 初始模型:记录单车位置
首先,我们定义系统的初始状态。为了更符合现实情况,我们假设共有 120 辆单车,初始时校园有 100 辆,地铁站有 20 辆。
# 初始化状态:字典是最简单的数据结构
state = {
'campus': 100,
'metro': 20
}
如果有一个人把车从校园骑到了地铁站,校园的车会少一辆,地铁站的车会多一辆。我们可以写一个简单的函数来描述这个过程:
def bike_to_metro(state):
"""将一辆车从校园移动到地铁站"""
state['campus'] -= 1
state['metro'] += 1
同理,我们也可以定义 bike_to_campus 函数。
2. 引入随机性:模拟人流
现实中,人们不会按照固定的时间表出现。我们可以假设每一分钟内:
* 校园有一个人取车去地铁站的概率是 p1 (例如 0.5)。
* 地铁站有一个人取车去校园的概率是 p2 (例如 0.4)。
利用 numpy.random.random() 函数,我们可以模拟这种随机事件。如果 random() < p1,说明这一分钟内有人要从校园出发。
import numpy as np
def step(state, p1, p2):
"""模拟一个时间步(例如一分钟)"""
# 模拟从校园出发
if np.random.random() < p1:
bike_to_metro(state)
# 模拟从地铁站出发
if np.random.random() < p2:
bike_to_campus(state)
3. 时间演变:运行模拟
有了单步模拟函数 step,我们就可以通过循环来模拟一段时间(比如一小时,即 60 分钟)内系统的变化。
为了更直观地观察这个过程,我们制作了一个动态的可视化演示。在这个演示中,你可以实时看到单车数量的变化以及骑行者的移动。
你可以直接用代码来生成这个动画,完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import matplotlib.patches as patches
# ==========================================
# 共享单车系统仿真模型
# ==========================================
# 1. 系统参数
TOTAL_BIKES = 12
P_CAMPUS_TO_METRO = 0.5 # 校园 -> 地铁站 的概率 (每分钟)
P_METRO_TO_CAMPUS = 0.4 # 地铁站 -> 校园 的概率 (每分钟)
DURATION = 60 # 模拟时长 (分钟)
# 2. 初始化状态
# bikes_campus: 校园里的单车数
# bikes_metro: 地铁站里的单车数
state = {
'campus': 10,
'metro': 2,
'campus_history': [],
'metro_history': [],
'movements': [] # 记录每一帧的移动事件: None, 'c2m', 'm2c'
}
# 3. 模拟函数
def run_step(current_state):
# 记录历史
current_state['campus_history'].append(current_state['campus'])
current_state['metro_history'].append(current_state['metro'])
# 模拟移动
move = None
# 检查从校园到地铁站的借车请求
if np.random.random() < P_CAMPUS_TO_METRO:
if current_state['campus'] > 0:
current_state['campus'] -= 1
current_state['metro'] += 1
move = 'c2m'
# 检查从地铁站到校园的借车请求
if np.random.random() < P_METRO_TO_CAMPUS:
if current_state['metro'] > 0:
current_state['metro'] -= 1
current_state['campus'] += 1
move = 'm2c'
current_state['movements'].append(move)
# 运行完整模拟以获取数据
np.random.seed(42) # 固定种子保证结果可复现
sim_data = {
'campus': [10],
'metro': [2],
'movements': [None]
}
temp_state = {'campus': 10, 'metro': 2, 'campus_history': [], 'metro_history': [], 'movements': []}
for _ in range(DURATION):
run_step(temp_state)
sim_data['campus'].extend(temp_state['campus_history'])
sim_data['metro'].extend(temp_state['metro_history'])
sim_data['movements'].extend(temp_state['movements'])
# ==========================================
# 动态可视化 (Dashboard 风格)
# ==========================================
plt.style.use('dark_background')
fig = plt.figure(figsize=(12, 7))
gs = fig.add_gridspec(2, 2, height_ratios=[1.5, 1])
# --- 上半部分:实时场景模拟 ---
ax_map = fig.add_subplot(gs[0, :])
ax_map.set_xlim(0, 100)
ax_map.set_ylim(0, 40)
ax_map.set_title("Real-time Bike Sharing Monitor", color='white', fontsize=16, pad=10)
ax_map.axis('off')
# 绘制地点
# 校园 (左侧)
campus_rect = patches.FancyBboxPatch((5, 5), 25, 30, boxstyle="round,pad=0.5",
fc='#27ae60', ec='#2ecc71', alpha=0.3)
ax_map.add_patch(campus_rect)
ax_map.text(17.5, 30, "CAMPUS", ha='center', color='#2ecc71', fontsize=12, fontweight='bold')
text_campus_count = ax_map.text(17.5, 15, "", ha='center', color='white', fontsize=24, fontweight='bold')
# 地铁站 (右侧)
metro_rect = patches.FancyBboxPatch((70, 5), 25, 30, boxstyle="round,pad=0.5",
fc='#2980b9', ec='#3498db', alpha=0.3)
ax_map.add_patch(metro_rect)
ax_map.text(82.5, 30, "METRO STN", ha='center', color='#3498db', fontsize=12, fontweight='bold')
text_metro_count = ax_map.text(82.5, 15, "", ha='center', color='white', fontsize=24, fontweight='bold')
# 道路
ax_map.plot([30, 70], [20, 20], '-', color='#7f8c8d', lw=4, zorder=0)
ax_map.plot([30, 70], [20, 20], '--', color='white', lw=1, zorder=0)
# 骑行者图标 (初始隐藏)
rider = ax_map.text(50, 22, "🚴", ha='center', fontsize=30, color='#f1c40f', alpha=0)
# --- 下半部分:数据图表 ---
# 校园单车数量曲线
ax_chart = fig.add_subplot(gs[1, :])
ax_chart.set_xlim(0, DURATION)
ax_chart.set_ylim(0, TOTAL_BIKES + 2)
ax_chart.set_xlabel("Time (min)")
ax_chart.set_ylabel("Available Bikes")
ax_chart.grid(True, linestyle='--', alpha=0.2)
line_campus, = ax_chart.plot([], [], '-', color='#2ecc71', lw=2, label='Campus')
line_metro, = ax_chart.plot([], [], '-', color='#3498db', lw=2, label='Metro Station')
ax_chart.legend(loc='upper right', frameon=False)
# 时间指示器
time_text = ax_chart.text(0.02, 0.9, "", transform=ax_chart.transAxes, color='white')
def update(frame):
# 1. 更新计数文本
c_count = sim_data['campus'][frame]
m_count = sim_data['metro'][frame]
text_campus_count.set_text(f"{c_count}")
text_metro_count.set_text(f"{m_count}")
# 2. 更新骑行动画
# 获取当前分钟发生的移动事件
move = sim_data['movements'][frame]
if move == 'c2m': # 校园 -> 地铁
rider.set_text("🚴 ➤")
rider.set_x(40) # 简化的位置示意
rider.set_alpha(1)
rider.set_color('#2ecc71') # 绿色代表来自校园
elif move == 'm2c': # 地铁 -> 校园
rider.set_text("◀ 🚴")
rider.set_x(60)
rider.set_alpha(1)
rider.set_color('#3498db') # 蓝色代表来自地铁
else:
rider.set_alpha(0) # 没人骑车
# 3. 更新曲线图
line_campus.set_data(range(frame+1), sim_data['campus'][:frame+1])
line_metro.set_data(range(frame+1), sim_data['metro'][:frame+1])
time_text.set_text(f"Time: {frame} min")
return text_campus_count, text_metro_count, rider, line_campus, line_metro, time_text
# 生成动画
ani = FuncAnimation(fig, update, frames=DURATION+1, interval=100, blit=True)
ani.save('../images/02_bike_share_dynamic.gif', writer='pillow', fps=10)
print("Animation saved to ../images/02_bike_share_dynamic.gif")
动态演示效果:
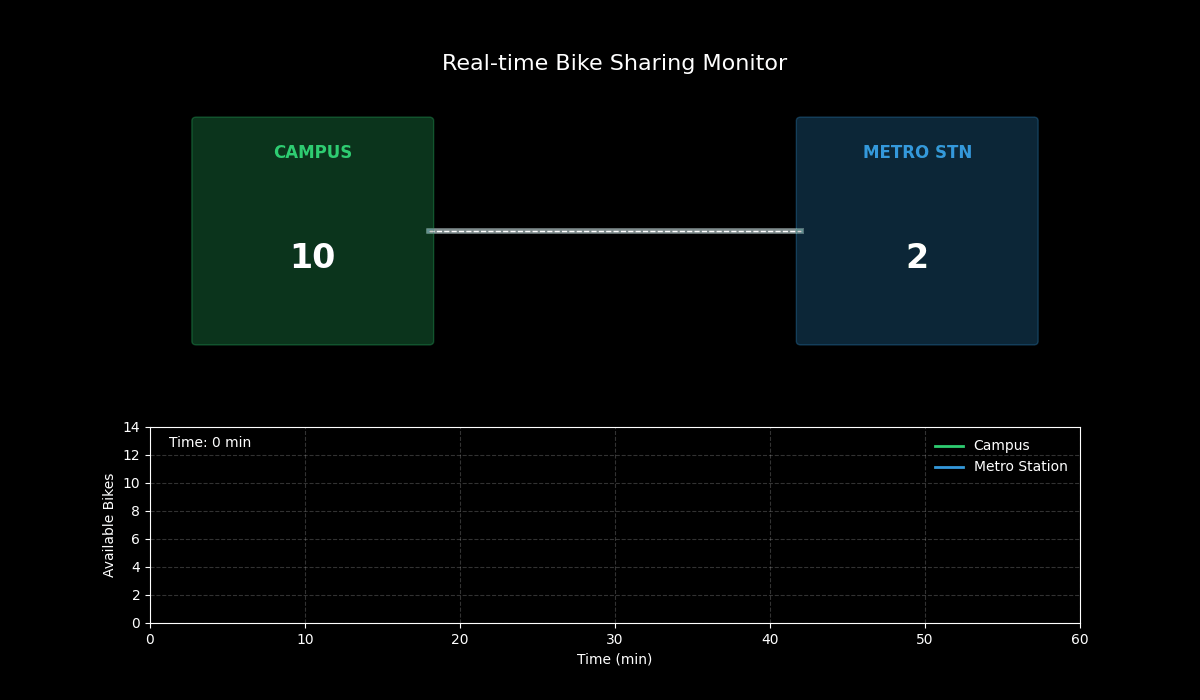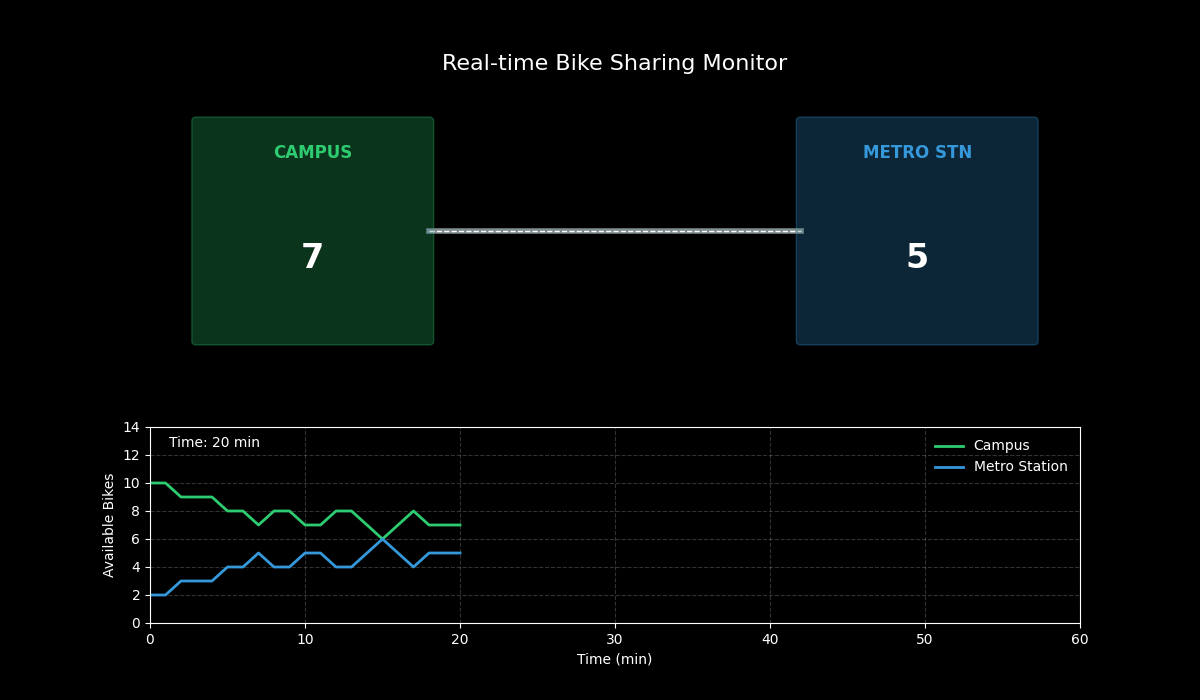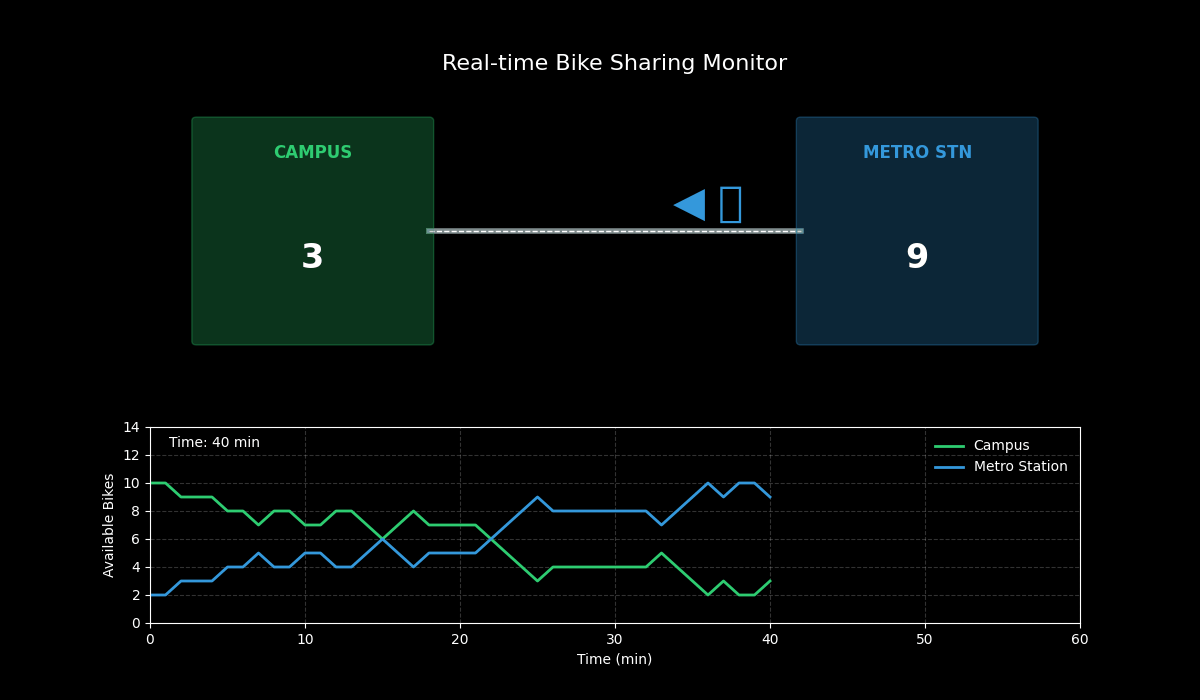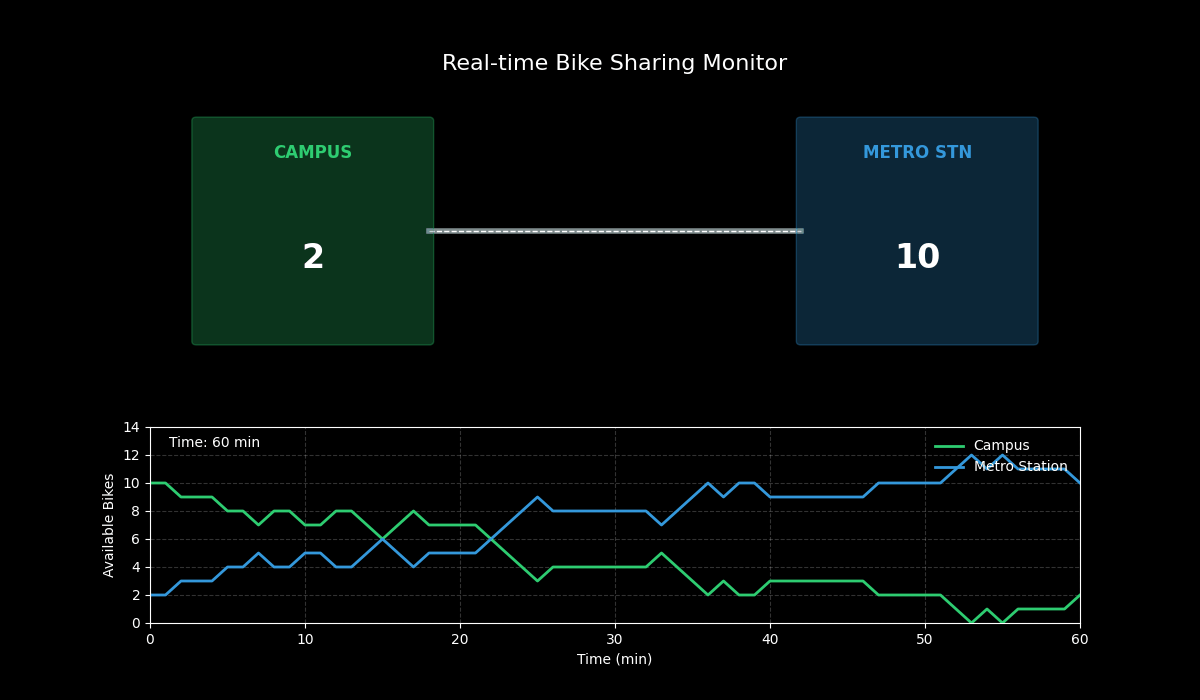
- 上半部分:展示了校园(左)和地铁站(右)的实时场景。中间的骑行者图标表示正在发生的移动事件。
- 下半部分:展示了两个地点单车数量随时间的实时变化曲线。
4. 完善模型:处理“无车可用”的情况
上面的模型有一个明显的漏洞:如果校园已经没车了(Campus = 0),函数 bike_to_MetroStn 仍然会执行减一操作,导致车数变成负数。这在物理上是不可能的。
我们需要修改移动车辆的函数,加入检查逻辑。如果没车了,就记录一次“不满意的客户”(Unsatisfied Customer),直接返回,不再减车。
def bike_to_MetroStn(state):
"""尝试将一辆车从校园移动到地铁站"""
if state.Campus == 0:
state.Campus_empty += 1 # 记录不满意的客户
return
state.Campus -= 1
state.MetroStn += 1
这样,Campus_empty 和 MetroStn_empty 就成了我们评估系统服务质量的重要指标。
可视化展示与参数扫视
模拟结果可视化
运行 run_simulation(0.3, 0.2, 60),我们可以得到一张图表,显示校园校园内单车数量随时间的变化。由于引入了随机性,每次运行生成的曲线都会有所不同,呈锯齿状波动。
参数扫视(Parameter Sweep)
仅仅运行一次模拟是不够的。我们想知道,不同的借车概率(p1)对系统服务质量到底有多大影响?比如,当校园的借车需求增加时,不满意的客户数量会如何变化?
这就需要进行参数扫视。我们让 p1 从 0 到 0.8 逐步变化,观察“校园不满意的客户数”这个指标。为了减少随机波动,我们在每个参数点上重复运行 20 次模拟取平均值。
你可以运行代码来生成参数扫视的动态演示,完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# ==========================================
# 参数扫视模拟
# ==========================================
TOTAL_BIKES = 12
DURATION = 60
NUM_SIMULATIONS = 20 # 每个参数值重复模拟的次数 (用于平滑曲线)
P2 = 0.4 # 地铁站 -> 校园 的固定概率
# 借车概率 (校园 -> 地铁) 范围:0 到 0.8
p1_array = np.linspace(0, 0.8, 41)
# 存储结果:每个 p1 对应的不满意客户数 (平均值)
sweep_results = []
current_p1_index = 0
def run_simulation(p1, p2, num_steps):
state = {'campus': 10, 'metro': 2, 'unhappy': 0}
for _ in range(num_steps):
# 校园 -> 地铁
if np.random.random() < p1:
if state['campus'] > 0:
state['campus'] -= 1
state['metro'] += 1
else:
state['unhappy'] += 1
# 地铁 -> 校园
if np.random.random() < p2:
if state['metro'] > 0:
state['metro'] -= 1
state['campus'] += 1
# 这里简化,不统计地铁站的不满意客户
return state['unhappy']
# ==========================================
# 动态可视化
# ==========================================
plt.style.use('dark_background')
fig, ax = plt.subplots(figsize=(10, 6))
ax.set_xlim(0, 0.8)
ax.set_ylim(0, 15)
ax.set_xlabel("Request Rate at Campus (p1)")
ax.set_ylabel("Average Unhappy Customers")
ax.set_title("Impact of Request Rate on Service Quality", fontsize=14, color='white', pad=20)
ax.grid(True, linestyle='--', alpha=0.3)
# 绘制曲线
line, = ax.plot([], [], 'o-', color='#e74c3c', lw=2, markersize=6, label='Unhappy Customers')
ax.legend(loc='upper left', frameon=False)
# 动态文本
text_param = ax.text(0.05, 0.8, "", transform=ax.transAxes, color='white', fontsize=12)
text_result = ax.text(0.05, 0.75, "", transform=ax.transAxes, color='#e74c3c', fontsize=14, fontweight='bold')
# 进度条背景
ax_progress = fig.add_axes([0.15, 0.02, 0.7, 0.03]) # [left, bottom, width, height]
ax_progress.set_xlim(0, 1)
ax_progress.set_ylim(0, 1)
ax_progress.axis('off')
rect_bg = plt.Rectangle((0, 0), 1, 1, fc='#34495e', ec=None)
ax_progress.add_patch(rect_bg)
rect_progress = plt.Rectangle((0, 0), 0, 1, fc='#2ecc71', ec=None)
ax_progress.add_patch(rect_progress)
ax_progress.text(0.5, 0.5, "Simulation Progress", ha='center', va='center', color='white', fontsize=8)
def update(frame):
global current_p1_index
if current_p1_index < len(p1_array):
p1 = p1_array[current_p1_index]
# 运行多次模拟取平均值
total_unhappy = 0
for _ in range(NUM_SIMULATIONS):
total_unhappy += run_simulation(p1, P2, DURATION)
avg_unhappy = total_unhappy / NUM_SIMULATIONS
sweep_results.append(avg_unhappy)
# 更新曲线
line.set_data(p1_array[:len(sweep_results)], sweep_results)
# 更新文本
text_param.set_text(f"Current p1 (Campus->Metro): {p1:.2f}")
text_result.set_text(f"Unhappy Customers: {avg_unhappy:.1f}")
# 更新进度条
progress = (current_p1_index + 1) / len(p1_array)
rect_progress.set_width(progress)
current_p1_index += 1
return line, text_param, text_result, rect_progress
# 生成动画
ani = FuncAnimation(fig, update, frames=len(p1_array)+10, interval=100, blit=True)
ani.save('../images/02_bike_share_sweep.gif', writer='pillow', fps=10)
print("Animation saved to ../images/02_bike_share_sweep.gif")
动态参数扫视效果:
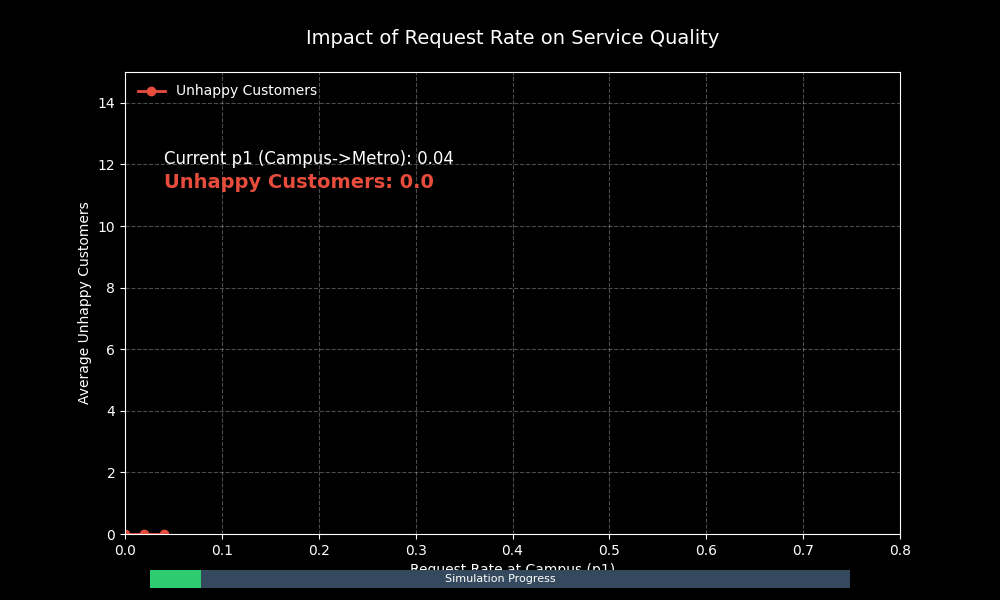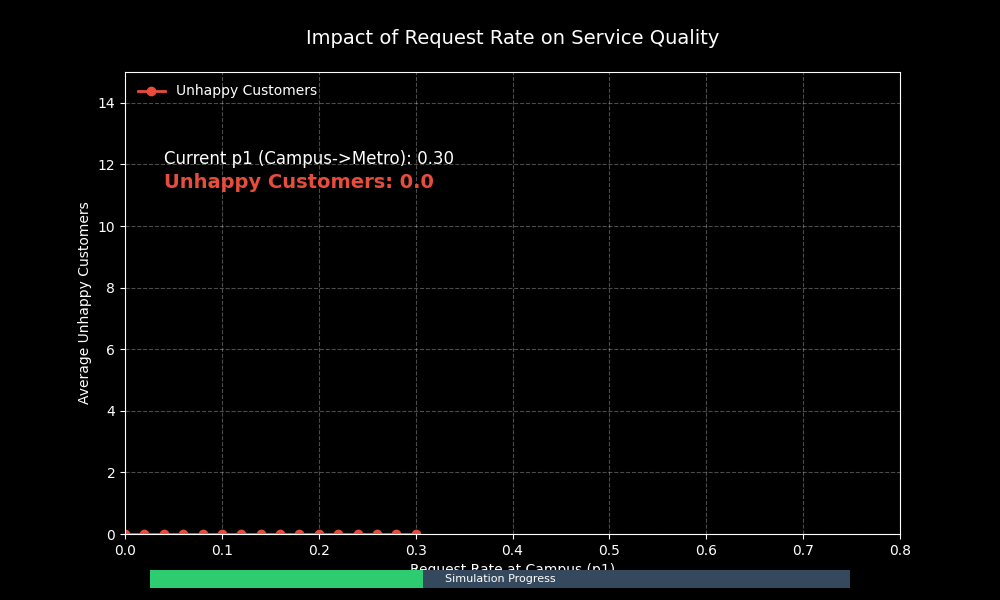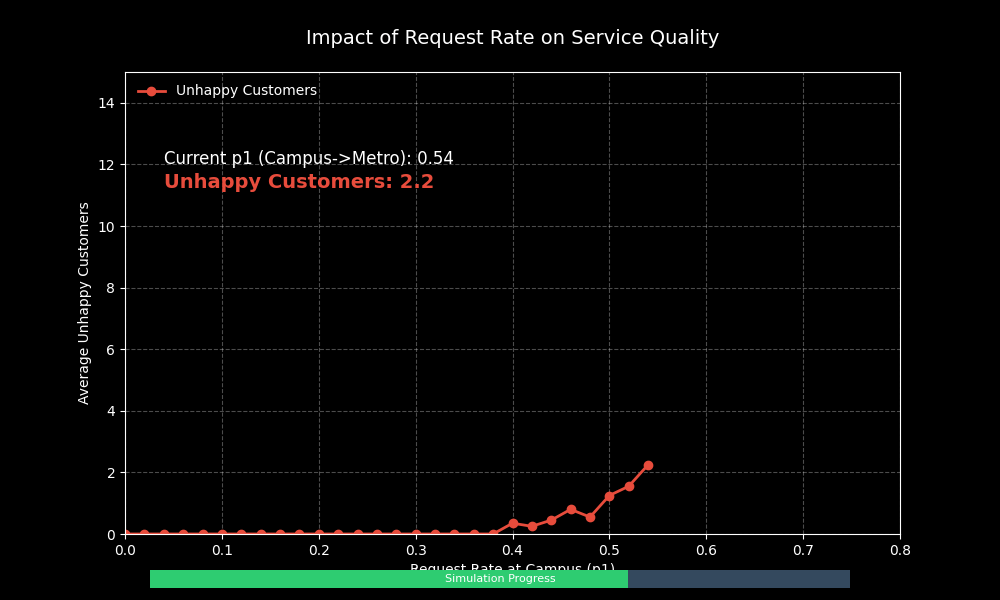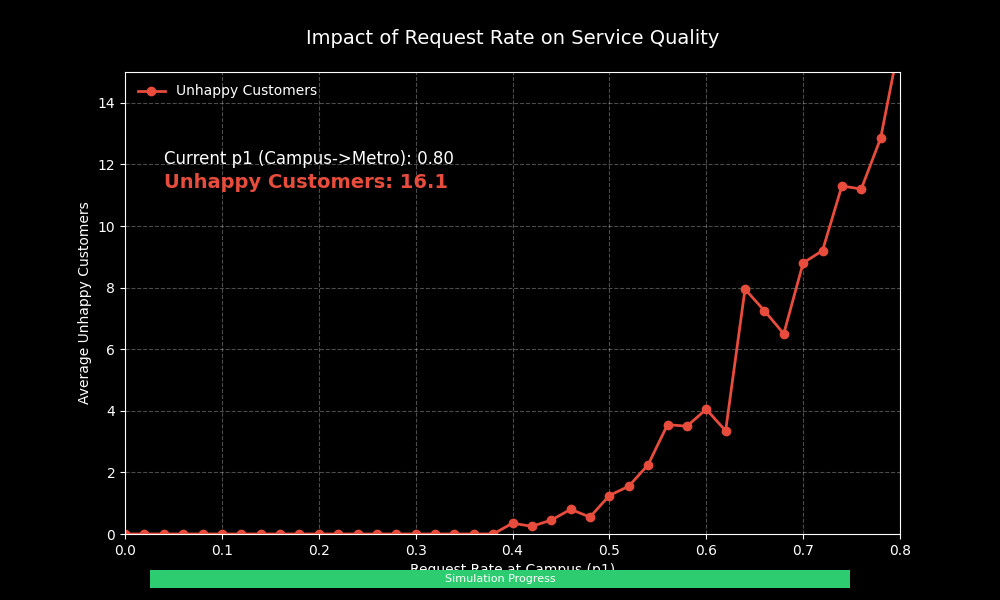
通过这张动态图,我们可以清晰地看到:
1. 当 p1 较小时(需求低),不满意客户数维持在 0 附近。
2. 随着 p1 增大,曲线开始出现非线性上升。这意味着一旦需求超过某个临界点,服务质量会急剧下降。
3. 这种“相变”现象提示我们,在设计系统容量时,必须留有足够的余量来应对高峰需求。
总结
通过这个共享单车系统的案例,我们完整地体验了建模的过程: 1. 从简单开始:先建立一个能跑通的最小模型(State 和基本移动函数)。 2. 迭代改进:发现问题(负数车辆),修改代码(增加条件判断),引入度量指标(不满意客户)。 3. 探索分析:使用参数扫视来分析系统行为随参数变化的规律。
这种迭代式建模(Iterative Modeling) 的方法,不仅适用于简单的共享单车系统,也是解决复杂工程和科学问题的有效路径。
 CycleUser
CycleUser