本系列受到 Allen B. Downey 的《Modeling and Simulation in Python》的启发,旨在通过 Python 编程语言,帮助新手同学来探索数学建模的基础内容。
知识背景
热力学是物理学中研究能量、热量、功、熵和自发过程的学科。对于初学者来说,内能(Internal Energy)、温度(Temperature)和压力(Pressure)这些概念往往比较抽象。
但在微观层面,这一切都变得非常直观: * 内能就是所有分子动能的总和。 * 温度是分子平均动能的量度。 * 压力是大量分子频繁撞击容器壁所产生的平均力。
在本章中,我们将通过构建一个理想气体分子动力学(Molecular Dynamics, MD)模型,从微观粒子的随机运动出发,模拟出一个宏观的隔热系统,并可视化其能量和压力的变化。
概念介绍
1. 理想气体模型
为了简化计算,我们假设: * 分子是刚性小球,只发生弹性碰撞。 * 分子之间没有相互作用力(除了碰撞瞬间)。 * 分子与容器壁发生弹性碰撞(动能守恒)。
2. 能量守恒(热力学第一定律)
在一个隔热(Adiabatic)的刚性容器中,系统与外界没有热量交换,也没有做功。根据热力学第一定律: $$\Delta U = Q - W = 0$$ 系统的总内能 $U$ 应当保持不变。
3. 压力的微观解释
压力 $P$ 定义为单位面积上受到的力 $F$。 $$P = \frac{F}{A}$$ 在微观上,力来自于分子撞击墙壁时的动量改变。根据牛顿第二定律: $$F = \frac{dp}{dt}$$ 因此,我们可以通过统计一段时间内所有分子撞击墙壁造成的动量变化总和,来计算瞬时压力。
代码实现
我们使用 Python 模拟 200 个气体分子在一个二维封闭容器中的运动。
核心算法
- 初始化:随机生成分子的位置和速度。
- 运动:在每个时间步
dt内,分子沿直线匀速运动。 - 碰撞检测:检查分子是否碰到墙壁。如果碰到,反转其垂直于墙壁的速度分量(弹性碰撞),并记录动量变化。
- 统计:计算当前的系统总动能和对墙壁的压力。
完整代码
你可以直接运行 code/05_gas_simulation.py 来生成模拟动画。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# 理想气体分子动力学模拟
# 1. 系统参数
N = 200 # 分子数量
BOX_SIZE = 10.0 # 容器边长
V_MAX = 2.0 # 最大初始速度
MASS = 1.0 # 分子质量
RADIUS = 0.1 # 分子半径
DT = 0.05 # 时间步长
STEPS = 500 # 模拟步数
# 2. 初始化状态
# 随机位置 (避开边界)
pos = np.random.uniform(RADIUS, BOX_SIZE - RADIUS, size=(N, 2))
# 随机速度
vel = np.random.uniform(-V_MAX, V_MAX, size=(N, 2))
# 存储历史数据用于绘图
history = {'pos': [], 'ke': [], 'pressure': []}
# 3. 模拟循环
def step(pos, vel):
# 更新位置
pos += vel * DT
# 碰撞检测:与墙壁碰撞 (弹性碰撞)
# x 方向边界
mask_x_left = pos[:, 0] < RADIUS
mask_x_right = pos[:, 0] > BOX_SIZE - RADIUS
# 动量变化用于计算压力 (F = dp/dt)
impulse = 0.0
if np.any(mask_x_left):
pos[mask_x_left, 0] = RADIUS
vel[mask_x_left, 0] *= -1
impulse += np.sum(2 * MASS * np.abs(vel[mask_x_left, 0]))
if np.any(mask_x_right):
pos[mask_x_right, 0] = BOX_SIZE - RADIUS
vel[mask_x_right, 0] *= -1
impulse += np.sum(2 * MASS * np.abs(vel[mask_x_right, 0]))
# y 方向边界
mask_y_bottom = pos[:, 1] < RADIUS
mask_y_top = pos[:, 1] > BOX_SIZE - RADIUS
if np.any(mask_y_bottom):
pos[mask_y_bottom, 1] = RADIUS
vel[mask_y_bottom, 1] *= -1
impulse += np.sum(2 * MASS * np.abs(vel[mask_y_bottom, 1]))
if np.any(mask_y_top):
pos[mask_y_top, 1] = BOX_SIZE - RADIUS
vel[mask_y_top, 1] *= -1
impulse += np.sum(2 * MASS * np.abs(vel[mask_y_top, 1]))
# 计算瞬时动能 (内能)
# KE = 0.5 * m * v^2
ke = 0.5 * MASS * np.sum(vel**2)
# 计算瞬时压力 (P = F/A, 这里是二维, P = F/L)
# F = impulse / DT
# L = 4 * BOX_SIZE
pressure = impulse / DT / (4 * BOX_SIZE)
return pos, vel, ke, pressure
# 运行模拟
for _ in range(STEPS):
pos, vel, ke, p = step(pos, vel)
history['pos'].append(pos.copy())
history['ke'].append(ke)
history['pressure'].append(p)
# 动态可视化
plt.style.use('dark_background')
fig = plt.figure(figsize=(12, 6))
gs = fig.add_gridspec(2, 2)
# --- 左图:气体分子运动 ---
ax_box = fig.add_subplot(gs[:, 0])
ax_box.set_xlim(0, BOX_SIZE)
ax_box.set_ylim(0, BOX_SIZE)
ax_box.set_aspect('equal')
ax_box.set_title("Ideal Gas Simulation (Adiabatic)", color='white', fontsize=14)
# 绘制容器边界
rect = plt.Rectangle((0, 0), BOX_SIZE, BOX_SIZE, ec='white', fc='none', lw=2)
ax_box.add_patch(rect)
# 绘制分子
particles, = ax_box.plot([], [], 'o', color='#3498db', markersize=4, alpha=0.8)
# --- 右上图:动能 (温度) ---
ax_temp = fig.add_subplot(gs[0, 1])
ax_temp.set_xlim(0, STEPS)
# 动能范围预估
ke_mean = np.mean(history['ke'])
ax_temp.set_ylim(ke_mean * 0.8, ke_mean * 1.2)
ax_temp.set_ylabel("Internal Energy (J)")
ax_temp.set_title("System Energy (Temperature)", color='white', fontsize=12)
line_ke, = ax_temp.plot([], [], '-', color='#e74c3c', lw=2)
# --- 右下图:压力 ---
ax_press = fig.add_subplot(gs[1, 1])
ax_press.set_xlim(0, STEPS)
ax_press.set_ylim(0, max(history['pressure']) * 1.2)
ax_press.set_ylabel("Pressure (Pa)")
ax_press.set_xlabel("Time Step")
ax_press.set_title("Wall Pressure", color='white', fontsize=12)
line_press, = ax_press.plot([], [], '-', color='#2ecc71', lw=1, alpha=0.6)
# 压力移动平均线
line_press_avg, = ax_press.plot([], [], '-', color='white', lw=2, label='Avg Pressure')
# 动画更新函数
def update(frame):
# 降采样:每 2 步取 1 帧
# 总步数 500 / 2 = 250 帧 < 300
skip = 2
idx = frame * skip
if idx >= STEPS: idx = STEPS - 1
# 1. 更新粒子位置
p = history['pos'][idx]
particles.set_data(p[:, 0], p[:, 1])
# 2. 更新能量曲线
line_ke.set_data(range(idx+1), history['ke'][:idx+1])
# 3. 更新压力曲线
press_data = history['pressure'][:idx+1]
line_press.set_data(range(idx+1), press_data)
# 计算压力的移动平均 (窗口大小 20)
if idx > 20:
avg_p = np.convolve(press_data, np.ones(20)/20, mode='valid')
line_press_avg.set_data(range(19, idx+1), avg_p)
return particles, line_ke, line_press, line_press_avg
frames = STEPS // 2
ani = FuncAnimation(fig, update, frames=frames, interval=30, blit=True)
ani.save('../images/05_gas_simulation.gif', writer='pillow', fps=20)
print("Simulation animation saved to ../images/05_gas_simulation.gif")
可视化结果与分析
下面的动态面板展示了模拟的全过程:
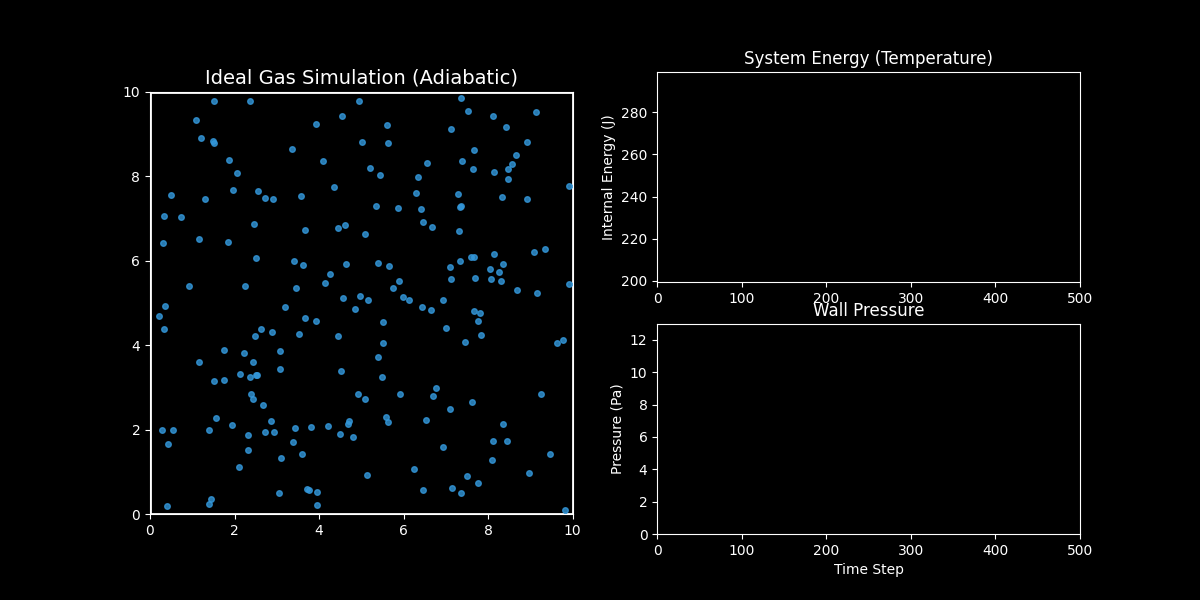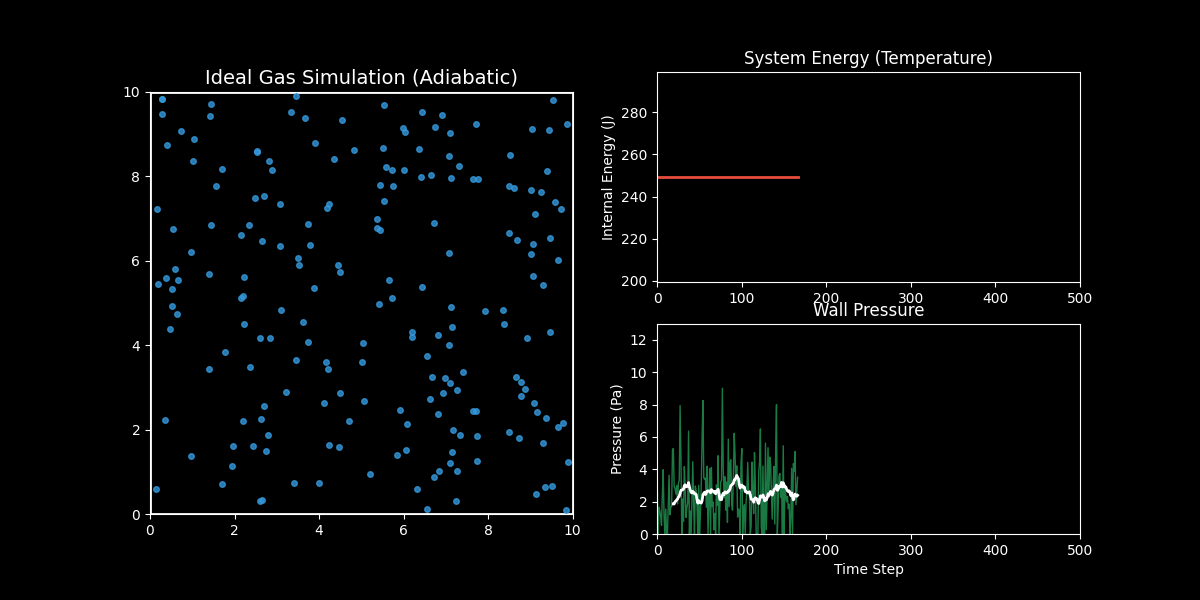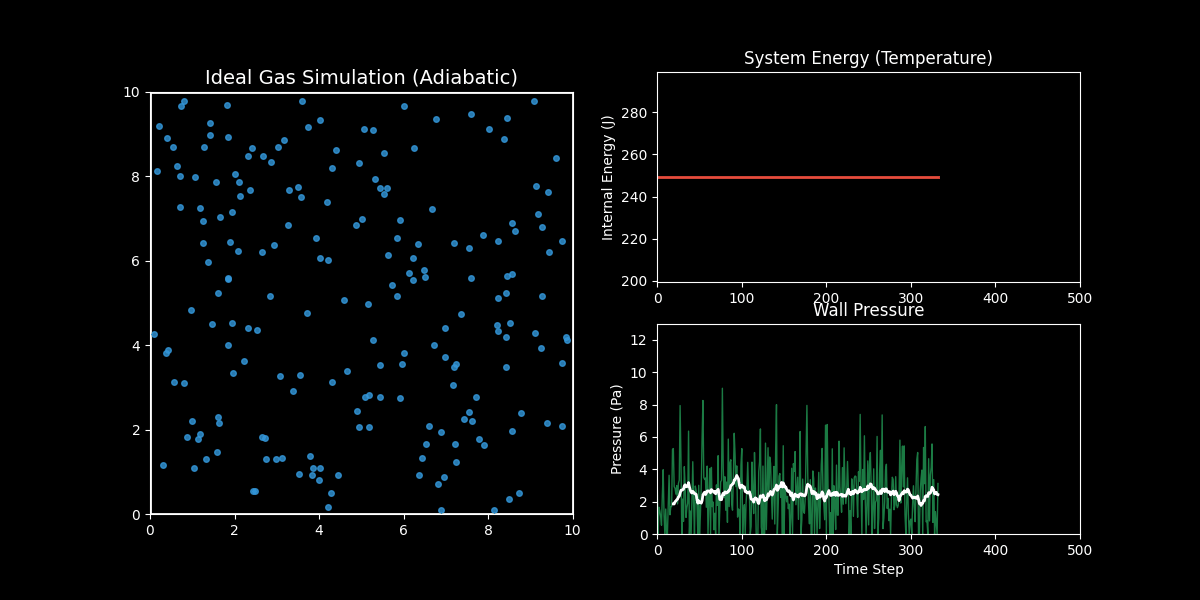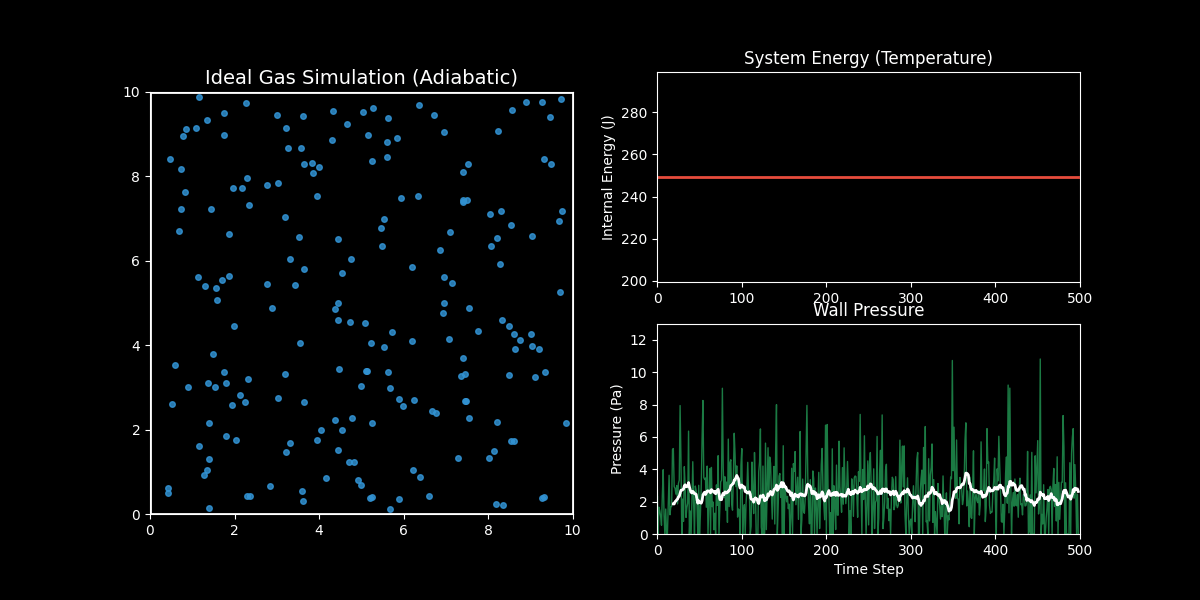
- 左图(分子运动):你可以看到蓝色的气体分子在容器内做无规则的热运动(布朗运动),并不断撞击墙壁。
- 右上图(内能/温度):红线显示了系统的总动能。你会发现它是一条完美的水平直线。这验证了能量守恒定律——在没有外力做功和热交换的情况下,理想气体的内能是恒定的。
- 右下图(压力):绿线是瞬时压力,白线是移动平均压力。虽然每个瞬间的撞击力度是随机波动的(噪声),但从统计平均来看,压力稳定在一个恒定的数值。这就解释了为什么宏观上我们能测量到稳定的气压。
绝热压缩与膨胀:活塞模型
在前面的模拟中,容器体积是固定的。现在,让我们引入一个可移动的活塞(Piston),通过改变容器体积来对气体做功。
1. 物理过程
- 压缩过程(Compression):活塞向内移动,分子撞击活塞时会被反弹回来,且速度增加(类似于你用网球拍击球,球速会变快)。外界对气体做功,气体内能增加,温度升高。
- 膨胀过程(Expansion):活塞向外移动,分子撞击活塞时反弹速度减小(类似于球打在后退的球拍上)。气体对外界做功,内能减少,温度降低。
2. 代码实现
我们需要修改碰撞检测逻辑,处理动墙(Moving Wall)碰撞: $$v_{new} = 2v_{wall} - v_{old}$$ 其中 $v_{wall}$ 是活塞速度。
完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# 理想气体绝热压缩/膨胀模拟
# 1. 系统参数
N = 100 # 分子数量
BOX_WIDTH_INIT = 10.0
BOX_HEIGHT = 10.0
V_MAX = 2.0 # 初始速度
MASS = 1.0
RADIUS = 0.1
DT = 0.05
STEPS = 600
# 活塞运动参数
PISTON_SPEED = 0.02 # 活塞速度 (正值压缩,负值膨胀)
# 我们设计一个周期运动:压缩 -> 膨胀
def get_piston_pos(step):
# 简单的正弦运动模拟活塞
# 周期 600 步
phase = step / STEPS * 2 * np.pi
# 宽度在 5.0 到 10.0 之间变化
return 7.5 + 2.5 * np.cos(phase)
def get_piston_vel(step):
# 位置的导数
phase = step / STEPS * 2 * np.pi
return -2.5 * np.sin(phase) * (2 * np.pi / STEPS / DT)
# 2. 初始化状态
pos = np.random.uniform(RADIUS, BOX_WIDTH_INIT - RADIUS, size=(N, 2))
pos[:, 1] = np.random.uniform(RADIUS, BOX_HEIGHT - RADIUS, size=N) # y 轴范围固定
vel = np.random.uniform(-V_MAX, V_MAX, size=(N, 2))
# 存储历史
history = {'pos': [], 'ke': [], 'pressure': [], 'volume': [], 'box_width': []}
# 3. 模拟循环
for step_idx in range(STEPS):
# 当前容器宽度 (由活塞位置决定)
current_width = get_piston_pos(step_idx)
next_width = get_piston_pos(step_idx + 1)
# 活塞瞬时速度
v_piston = (next_width - current_width) / DT
# 更新分子位置
pos += vel * DT
# 碰撞检测
impulse = 0.0
# --- 右侧活塞墙壁 (动墙) ---
# 只有 x > current_width - RADIUS 的分子可能碰撞
mask_piston = pos[:, 0] > current_width - RADIUS
if np.any(mask_piston):
# 修正位置
pos[mask_piston, 0] = current_width - RADIUS
# 弹性碰撞公式 (动墙)
# v_new = 2 * v_wall - v_old
# 这里 v_wall = v_piston
v_old_x = vel[mask_piston, 0]
v_new_x = 2 * v_piston - v_old_x
vel[mask_piston, 0] = v_new_x
# 动量变化 (相对于静止参考系)
# 但计算压力时通常用相对动量变化,或者直接用 F = ma
# 这里简化:压力来自于分子对活塞的冲量
# 冲量 I = m * (v_new - v_old)
impulse += np.sum(MASS * np.abs(v_new_x - v_old_x))
# --- 左侧、上侧、下侧 (静墙) ---
mask_left = pos[:, 0] < RADIUS
if np.any(mask_left):
pos[mask_left, 0] = RADIUS
vel[mask_left, 0] *= -1
mask_bottom = pos[:, 1] < RADIUS
if np.any(mask_bottom):
pos[mask_bottom, 1] = RADIUS
vel[mask_bottom, 1] *= -1
mask_top = pos[:, 1] > BOX_HEIGHT - RADIUS
if np.any(mask_top):
pos[mask_top, 1] = BOX_HEIGHT - RADIUS
vel[mask_top, 1] *= -1
# 记录数据
ke = 0.5 * MASS * np.sum(vel**2)
pressure = impulse / DT / BOX_HEIGHT # 只计算活塞受到的压力 P=F/L
history['pos'].append(pos.copy())
history['ke'].append(ke)
history['pressure'].append(pressure)
history['box_width'].append(current_width)
history['volume'].append(current_width * BOX_HEIGHT)
# 动态可视化
plt.style.use('dark_background')
fig = plt.figure(figsize=(10, 10))
# 调整布局,增加 hspace 防止重叠
gs = fig.add_gridspec(3, 1, height_ratios=[2, 1, 1], hspace=0.4)
# --- 上图:活塞运动 ---
ax_box = fig.add_subplot(gs[0])
ax_box.set_xlim(0, 12)
ax_box.set_ylim(0, 10)
ax_box.set_aspect('equal')
ax_box.set_title("Adiabatic Compression/Expansion", color='white', fontsize=14)
ax_box.set_xlabel("Volume Change (Piston Movement)")
# 容器边界
wall_top = ax_box.axhline(BOX_HEIGHT, color='white', lw=2)
wall_bottom = ax_box.axhline(0, color='white', lw=2)
wall_left = ax_box.axvline(0, color='white', lw=2)
# 活塞
piston_line = ax_box.axvline(BOX_WIDTH_INIT, color='#e74c3c', lw=4, label='Piston')
# 分子
particles, = ax_box.plot([], [], 'o', color='#3498db', markersize=5, alpha=0.8)
# --- 中图:温度 (动能) ---
ax_temp = fig.add_subplot(gs[1])
ax_temp.set_xlim(0, STEPS)
ax_temp.set_ylim(np.min(history['ke'])*0.8, np.max(history['ke'])*1.2)
ax_temp.set_ylabel("Internal Energy (Temp)")
ax_temp.grid(True, linestyle='--', alpha=0.3)
line_ke, = ax_temp.plot([], [], '-', color='#f1c40f', lw=2)
# --- 下图:压力 ---
ax_press = fig.add_subplot(gs[2])
ax_press.set_xlim(0, STEPS)
ax_press.set_ylim(0, np.max(history['pressure'])*1.5)
ax_press.set_ylabel("Pressure on Piston")
ax_press.set_xlabel("Time Step")
ax_press.grid(True, linestyle='--', alpha=0.3)
line_press, = ax_press.plot([], [], '-', color='#2ecc71', lw=1, alpha=0.5)
line_press_avg, = ax_press.plot([], [], '-', color='white', lw=2)
def update(frame):
# 降采样:每 3 步取 1 帧
# 总步数 600 / 3 = 200 帧 < 300
skip = 3
idx = frame * skip
if idx >= STEPS: idx = STEPS - 1
# 1. 更新活塞和分子
width = history['box_width'][idx]
piston_line.set_xdata([width, width])
p = history['pos'][idx]
particles.set_data(p[:, 0], p[:, 1])
# 2. 更新曲线
# xdata 对应模拟步数,而不是帧数
current_step = idx
xdata = range(current_step + 1)
line_ke.set_data(xdata, history['ke'][:current_step+1])
press_data = history['pressure'][:current_step+1]
line_press.set_data(xdata, press_data)
if current_step > 10:
avg_p = np.convolve(press_data, np.ones(10)/10, mode='valid')
line_press_avg.set_data(range(9, current_step+1), avg_p)
return piston_line, particles, line_ke, line_press, line_press_avg
frames = STEPS // 3
ani = FuncAnimation(fig, update, frames=frames, interval=30, blit=True)
ani.save('../images/05_piston_simulation.gif', writer='pillow', fps=20)
print("Piston animation saved to ../images/05_piston_simulation.gif")
3. 可视化结果
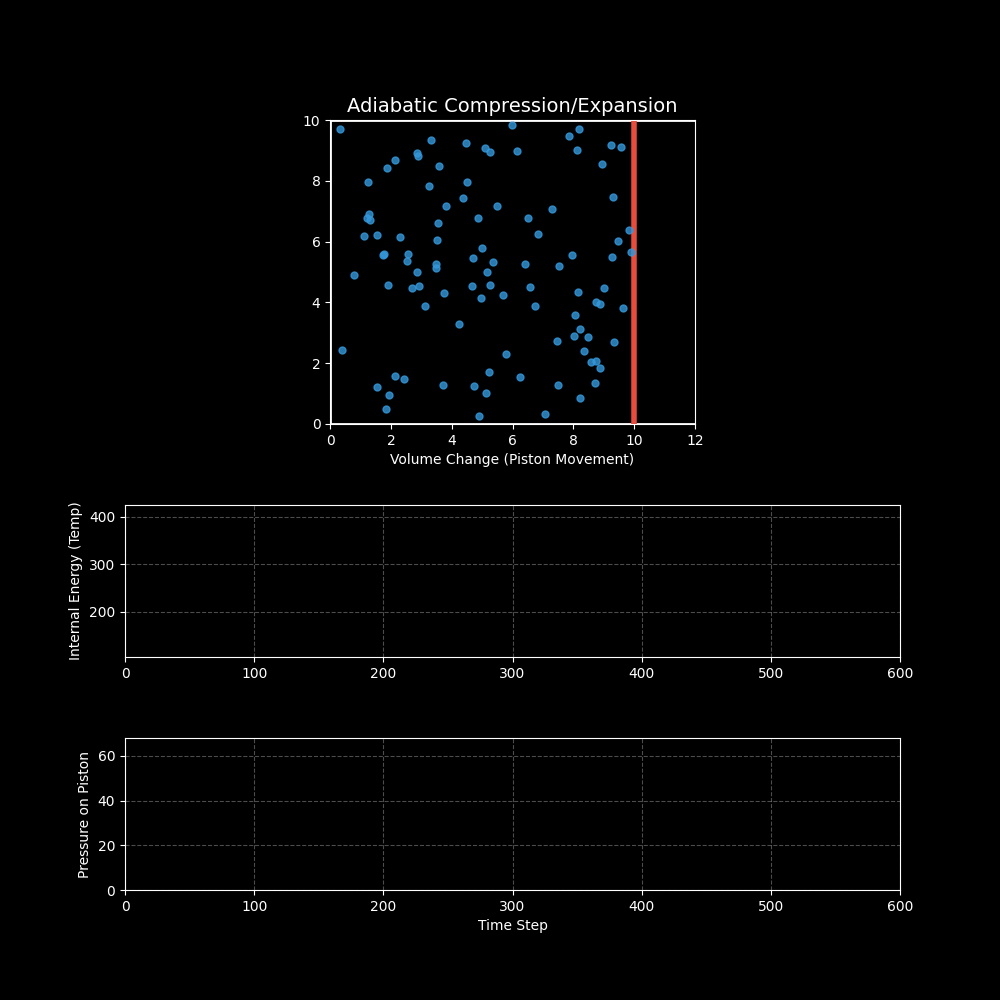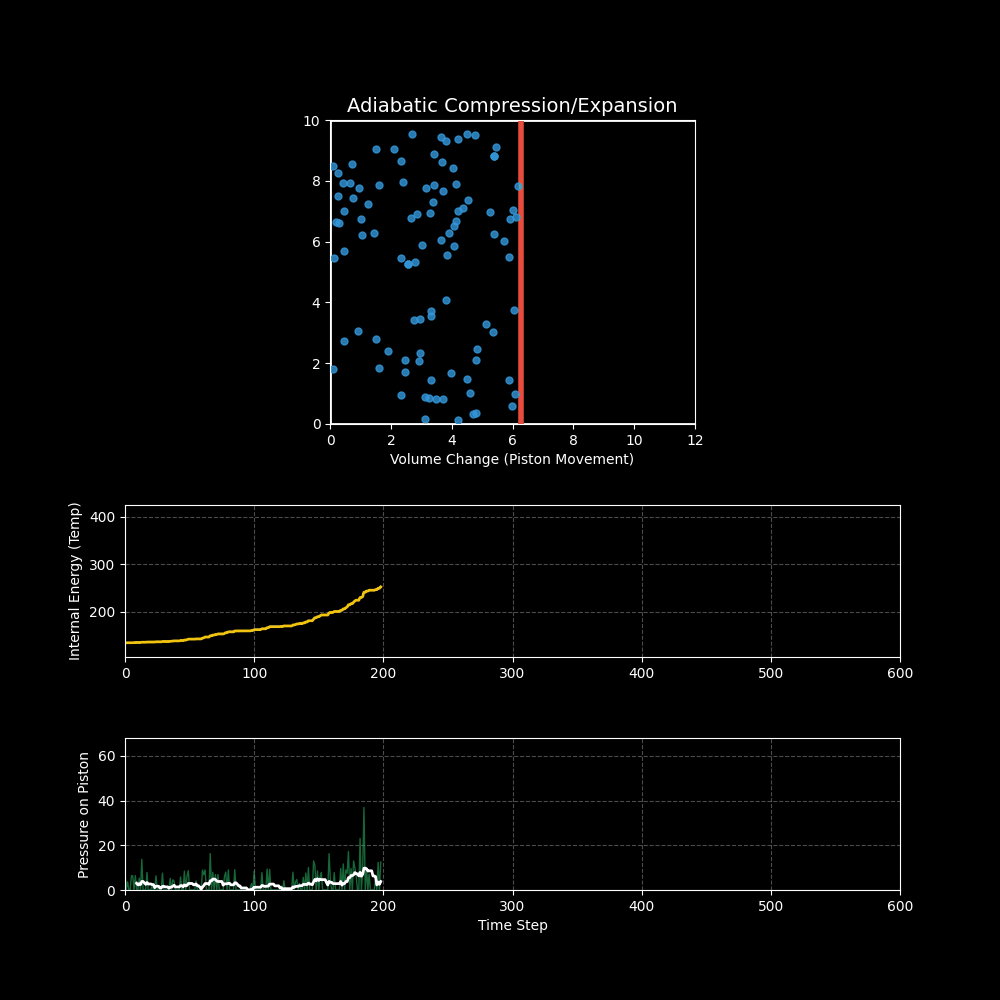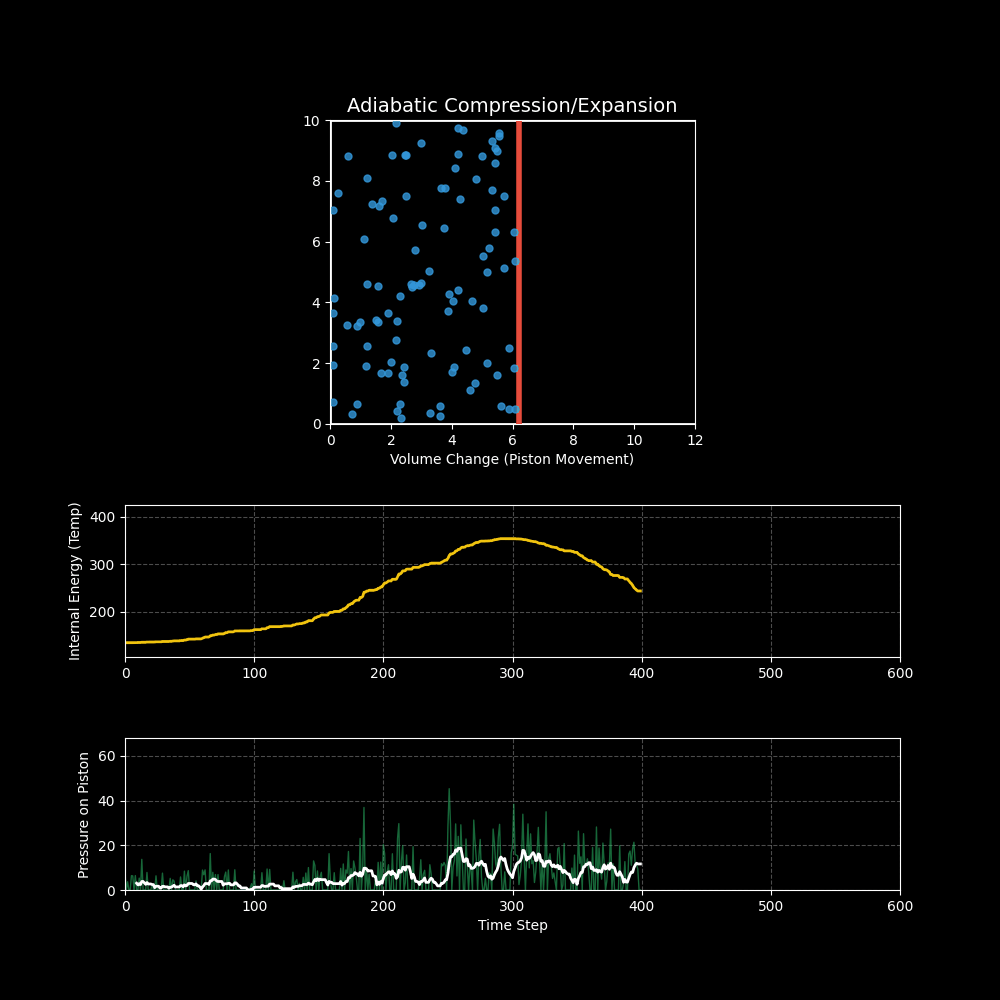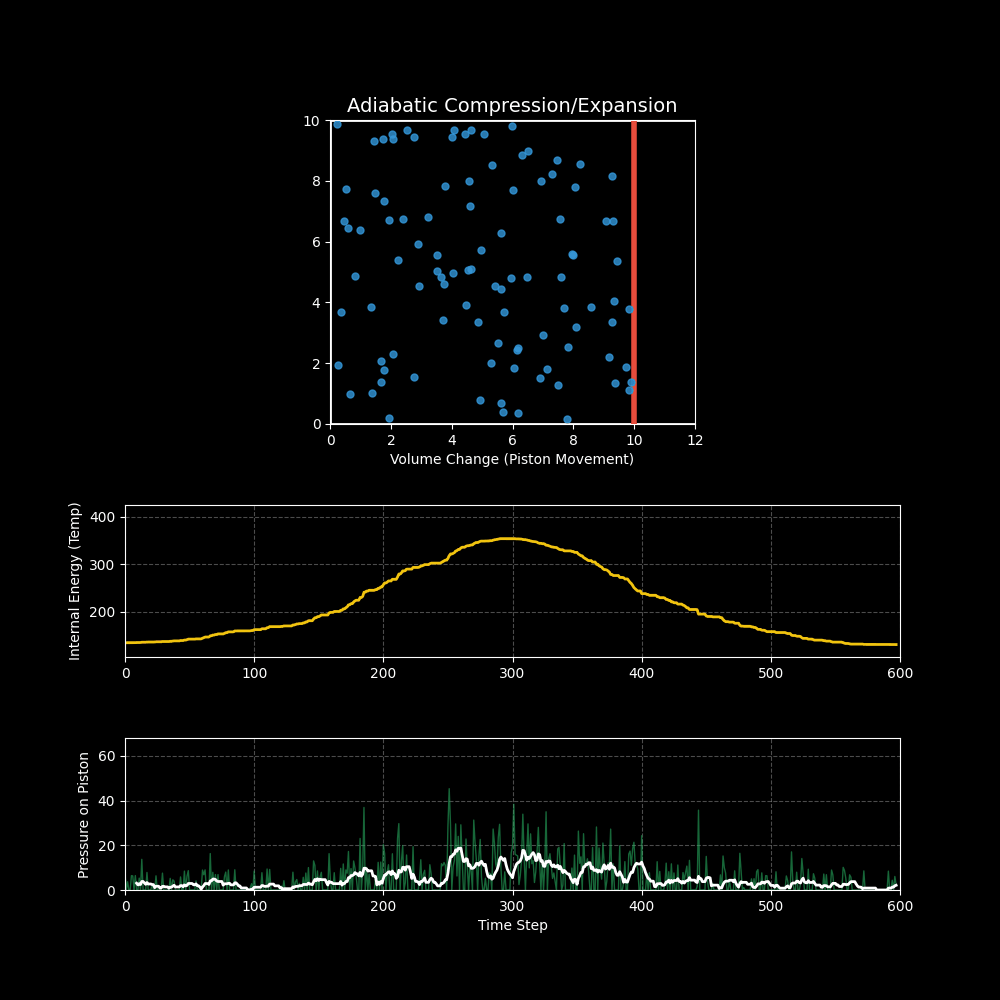
- 上图:展示了活塞(红线)的周期性运动。你可以看到当活塞向左压缩时,分子运动明显变剧烈;当活塞向右膨胀时,分子运动变缓慢。
- 中图(温度/内能):黄线显示了系统的温度变化。压缩升温,膨胀降温,这正是柴油发动机点火(压缩引燃)和冰箱制冷(膨胀吸热)的基本原理。
- 下图(压力):绿线显示了气体对活塞的压力。体积越小,压力越大(波义耳定律),且温度升高进一步加剧了压力的上升。
总结
通过这个模拟,我们成功地架起了微观粒子运动与宏观热力学定律之间的桥梁: 1. 微观随机性(分子的混乱运动)导致了宏观稳定性(稳定的压力和温度)。 2. 能量守恒在微观碰撞中得到了严格的体现。 3. 压力本质上是大量分子撞击效应的统计平均。
这种分子动力学模拟方法不仅可以用于理想气体,通过引入分子间作用力(如 Lennard-Jones 势),还可以模拟液体、固体甚至相变过程。
 CycleUser
CycleUser