本系列受到 Allen B. Downey 的《Modeling and Simulation in Python》的启发,旨在通过 Python 编程语言,帮助新手同学来探索数学建模的基础内容。
知识背景
1987年,三位物理学家 Per Bak、Chao Tang 和 Kurt Wiesenfeld 在《物理评论快报》上发表了一篇看似简单的论文 [1]。他们用计算机模拟了一个沙堆,揭示了一个道理:复杂系统不需要外部的精细调节,就能自发演化到临界状态。小崩塌频繁发生,大崩塌偶尔出现,崩塌规模服从幂律分布——这种规律在地震、森林火灾、股票市场崩溃中都能观察到。
这个发现被称为自组织临界性(Self-Organized Criticality),它为理解自然界中的复杂现象提供了一个优雅的理论框架。
概念介绍
Bak、Tang 和 Wiesenfeld 提出的这个沙堆模型(后文简称 BTW 模型)是一个定义在二维网格上的元胞自动机。想象一个棋盘,每个格子可以存放若干粒沙子。规则极其简单:假设每个沙粒都是一个小方块,上面能稳定摞起来最多4个沙粒;当某个格子的沙粒数达到或超过 4 时,这个格子就会"崩塌"——减少 4 粒沙,分别分给上下左右四个邻居各 1 粒;超出沙堆的视图边界之外的沙粒直接视为丢失。
这个规则看似平淡无奇,却蕴含着深刻的物理意义。崩塌可能触发邻居的崩塌,邻居的崩塌又可能触发更远的崩塌,形成连锁反应——这就是"雪崩"效应。系统会在没有外部干预的情况下,自发达到一个临界状态:大部分时候风平浪静,偶尔却会因为一粒沙引发波及整个系统的巨大崩塌。
Dhar 后来证明了该模型的一个重要性质:最终稳定态与崩塌的顺序无关 [2]。假设有两个不稳定的格子 A 和 B,先崩塌 A 再崩塌 B,与先崩塌 B 再崩塌 A,最终得到的稳定态完全相同。这种"操作顺序不影响结果"的特性,在数学上称为阿贝尔性质——得名于挪威数学家阿贝尔(Niels Henrik Abel),他在群论中研究了满足交换律 a + b = b + a 的运算结构。沙堆模型的崩塌操作恰好满足这种交换性,因此可以并行处理所有不稳定的格子,大大简化了模拟的复杂度。
代码实现
我们使用 Python 来实现这个模型。核心思路是用 NumPy 的向量化操作来处理崩塌过程,避免低效的循环遍历。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.colors import LinearSegmentedColormap
# 参数设置
GRID_SIZE = 40 # 设置沙盘尺寸为40*40
N_FRAMES = 10000 # 一共进行的次数
THRESHOLD = 4 # 设置超过4就会崩塌
# 高效沙堆模拟 (向量化实现)
class Sandpile:
def __init__(self, size):
self.size = size
self.grid = np.zeros((size, size), dtype=np.int32)
self.total_grains = 0
def add_grain(self):
"""在中心添加一粒沙"""
self.grid[self.size // 2, self.size // 2] += 1
self.total_grains += 1
def topple_vectorized(self):
"""向量化崩塌 - 高效实现"""
while np.any(self.grid >= THRESHOLD):
# 找出所有不稳定位置
unstable = self.grid >= THRESHOLD
# 崩塌数量 (整除)
topples = self.grid // THRESHOLD
# 减去崩塌的沙粒
self.grid -= topples * THRESHOLD
# 向量化分配给四个邻居
self.grid[1:, :] += topples[:-1, :] # 上方邻居
self.grid[:-1, :] += topples[1:, :] # 下方邻居
self.grid[:, 1:] += topples[:, :-1] # 左边邻居
self.grid[:, :-1] += topples[:, 1:] # 右边邻居
# 边界溢出丢失 (已在上面自动处理)
def step(self):
"""一步演化"""
self.add_grain()
self.topple_vectorized()
# 颜色映射 (黑色背景 → 灰度 → 蓝白)
colors = ['#000000', '#1a1a1a', '#333333', '#4d4d4d', '#666666',
'#5c7a99', '#4a90b8', '#38a6d6', '#66c2e0', '#99d9f0',
'#ccebfa', '#e6f5ff', '#ffffff']
cmap = LinearSegmentedColormap.from_list('sand', colors, N=256)
# 预计算所有帧 (采样以保持在300帧以内)
MAX_FRAMES = 270
step_per_frame = max(1, N_FRAMES // MAX_FRAMES)
actual_frames = N_FRAMES // step_per_frame
print(f"模拟 {N_FRAMES} 步, 每 {step_per_frame} 步保存一帧...")
sandpile = Sandpile(GRID_SIZE)
frames_data = [sandpile.grid.copy()]
for i in range(N_FRAMES):
sandpile.step()
if (i + 1) % step_per_frame == 0:
frames_data.append(sandpile.grid.copy())
if (i + 1) % 1000 == 0:
print(f" {i+1}/{N_FRAMES}")
print(f"完成! 共 {sandpile.total_grains} 沙粒, {len(frames_data)} 帧")
# 可视化
plt.style.use('dark_background')
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_aspect('equal')
ax.axis('off')
im = ax.imshow(frames_data[0], cmap=cmap, vmin=0, vmax=6,
interpolation='nearest', origin='lower')
title = ax.set_title('Sandpile: 0 grains', fontsize=14, color='white')
cbar = plt.colorbar(im, ax=ax, shrink=0.8)
cbar.set_label('Grains', color='white')
plt.tight_layout()
def update(frame):
im.set_array(frames_data[frame])
title.set_text(f'Sandpile: {frame} grains')
return [im, title]
ani = FuncAnimation(fig, update, frames=len(frames_data), interval=50, blit=True)
ani.save('../images/06_sandpile_avalanche.gif', writer='pillow', fps=256)
print(f"\n动画已保存: {len(frames_data)} 帧 @ 256 fps (总步数: {N_FRAMES})")
这段代码的核心在于 topple_vectorized 方法。传统的实现需要逐个检查每个格子、逐个更新邻居,效率极低。而向量化实现则一次性计算所有格子的崩塌量,利用数组切片操作批量更新邻居——将原本需要多次循环的操作压缩为几次矩阵运算。
可视化展示
上面的代码用动画展示沙堆从零开始逐步演化的完整过程。
观察这个动画,你会发现几个有趣的现象。刚开始时,沙粒堆在中心,周围一片漆黑。随着沙粒增多,一个圆形的"沙丘"逐渐形成。当某处的沙粒数超过临界值时,崩塌发生了——沙粒向四周扩散,可能触发新的崩塌,形成连锁反应。
最终,沙堆呈现出美丽的分形图案。黑色代表空格子,灰蓝色代表沙粒较少的区域,亮白色代表沙粒密集的区域。这些图案具有自相似性:无论放大多少倍,都能看到相似的结构——这正是临界态的标志。
分布
在讨论沙堆模型的统计特性之前,我们需要先理解两种截然不同的概率分布。
正态分布(高斯分布)是最常见的概率分布,描述了大量随机变量的叠加效应。其概率密度函数为
$$P(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$
其中 μ 是均值,σ 是标准差。正态分布的曲线呈钟形,中间高两头低,绝大多数数据集中在均值附近。人的身高、测量误差、考试成绩都近似服从正态分布。这种分布有一个明确的"特征尺度"——均值 μ 告诉我们"典型值"是多少,标准差 σ 告诉我们数据有多分散。超出三个标准差的事件极为罕见,几乎不可能发生。
幂律分布则完全不同。其概率密度函数为
$$P(x) = C x^{-\alpha}$$
其中 α 是幂律指数,C 是归一化常数。对两边取对数得到
$$\log P(x) = \log C - \alpha \log x$$
这表明在对数坐标系中,幂律分布表现为一条直线。与正态分布不同,幂律分布没有特征尺度——不存在所谓的"典型值"。小事件频繁发生,大事件偶尔出现,但两者遵循相同的统计规律。
下面咱们用一个代码对上面提到的两种分布的本体和双对数形态以及尾部特征都逐个进行可视化:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
plt.style.use('dark_background')
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# 左图: 正态分布 vs 幂律分布 (线性坐标)
ax1 = axes[0]
# 正态分布
mu, sigma = 0, 1
x_norm = np.linspace(-4, 4, 1000)
y_norm = norm.pdf(x_norm, mu, sigma)
ax1.plot(x_norm, y_norm, 'cyan', lw=2.5, label='Normal: μ=0, σ=1')
ax1.fill_between(x_norm, y_norm, alpha=0.3, color='cyan')
# 幂律分布 (截断版, 便于在同一图中展示)
x_power = np.linspace(0.1, 4, 1000)
alpha = 2.5
C = (alpha - 1) # 归一化常数, 使分布在 [1, ∞) 上积分为1
y_power = C * x_power ** (-alpha)
y_power_norm = y_power / np.max(y_power) * np.max(y_norm) # 缩放以便对比
ax1.plot(x_power, y_power_norm, 'orange', lw=2.5, label=f'Power Law: α={alpha}')
ax1.fill_between(x_power, y_power_norm, alpha=0.3, color='orange')
ax1.set_xlabel('x', fontsize=12)
ax1.set_ylabel('P(x)', fontsize=12)
ax1.set_title('Linear Scale', fontsize=14)
ax1.legend(loc='upper right', fontsize=10)
ax1.grid(True, alpha=0.3, ls='--')
ax1.set_xlim(-4, 4)
ax1.set_ylim(0, 0.5)
# 添加注释
ax1.annotate('Bell shape\n(Fast decay)', xy=(0, 0.4), fontsize=9,
color='cyan', ha='center')
ax1.annotate('Fat tail\n(Slow decay)', xy=(2.5, 0.15), fontsize=9,
color='orange', ha='center')
# 中图: 对数坐标对比
ax2 = axes[1]
# 正态分布 (对数坐标)
ax2.semilogy(x_norm[x_norm > -3], y_norm[x_norm > -3], 'cyan', lw=2.5, label='Normal')
# 幂律分布 (对数坐标)
ax2.loglog(x_power, y_power, 'orange', lw=2.5, label=f'Power Law (α={alpha})')
ax2.set_xlabel('x (log scale)', fontsize=12)
ax2.set_ylabel('P(x) (log scale)', fontsize=12)
ax2.set_title('Log-Log Scale', fontsize=14)
ax2.legend(loc='upper right', fontsize=10)
ax2.grid(True, alpha=0.3, ls='--', which='both')
# 添加关键特征注释
ax2.text(0.3, 0.5, 'Power Law:\nStraight line\non log-log plot',
transform=ax2.transAxes, fontsize=9, color='orange',
bbox=dict(boxstyle='round', facecolor='#1a1a1a', alpha=0.8))
ax2.text(0.6, 0.5, 'Normal:\nCurved downward\n(exponential decay)',
transform=ax2.transAxes, fontsize=9, color='cyan',
bbox=dict(boxstyle='round', facecolor='#1a1a1a', alpha=0.8))
# 右图: 尾部对比 (极端事件概率)
ax3 = axes[2]
# 扩展范围, 展示尾部行为
x_tail = np.linspace(1, 10, 500)
# 正态分布的尾部
y_norm_tail = norm.pdf(x_tail, 0, 1)
ax3.semilogy(x_tail, y_norm_tail, 'cyan', lw=2.5, label='Normal (σ=1)')
# 不同幂律指数的尾部
for alpha_val, color, ls in [(2.0, '#ff6b6b', '-'),
(2.5, 'orange', '-'),
(3.0, '#ffd93d', '-')]:
C_val = alpha_val - 1
y_power_tail = C_val * x_tail ** (-alpha_val)
ax3.semilogy(x_tail, y_power_tail, color=color, lw=2, linestyle=ls,
label=f'Power Law (α={alpha_val})')
ax3.set_xlabel('x', fontsize=12)
ax3.set_ylabel('P(x) (log scale)', fontsize=12)
ax3.set_title('Tail Behavior: Extreme Events', fontsize=14)
ax3.legend(loc='upper right', fontsize=9)
ax3.grid(True, alpha=0.3, ls='--', which='both')
# 添加关键区域标注
ax3.axvspan(5, 10, alpha=0.15, color='red')
ax3.text(7.5, 0.5, 'Extreme\nEvents\nZone', transform=ax3.transAxes,
fontsize=9, color='red', ha='center', va='center')
plt.tight_layout()
plt.subplots_adjust(bottom=0.12)
plt.savefig('../images/06_distribution_comparison.png', dpi=150, facecolor='black', edgecolor='none')
plt.show()
上述代码运行后效果如下图所示:
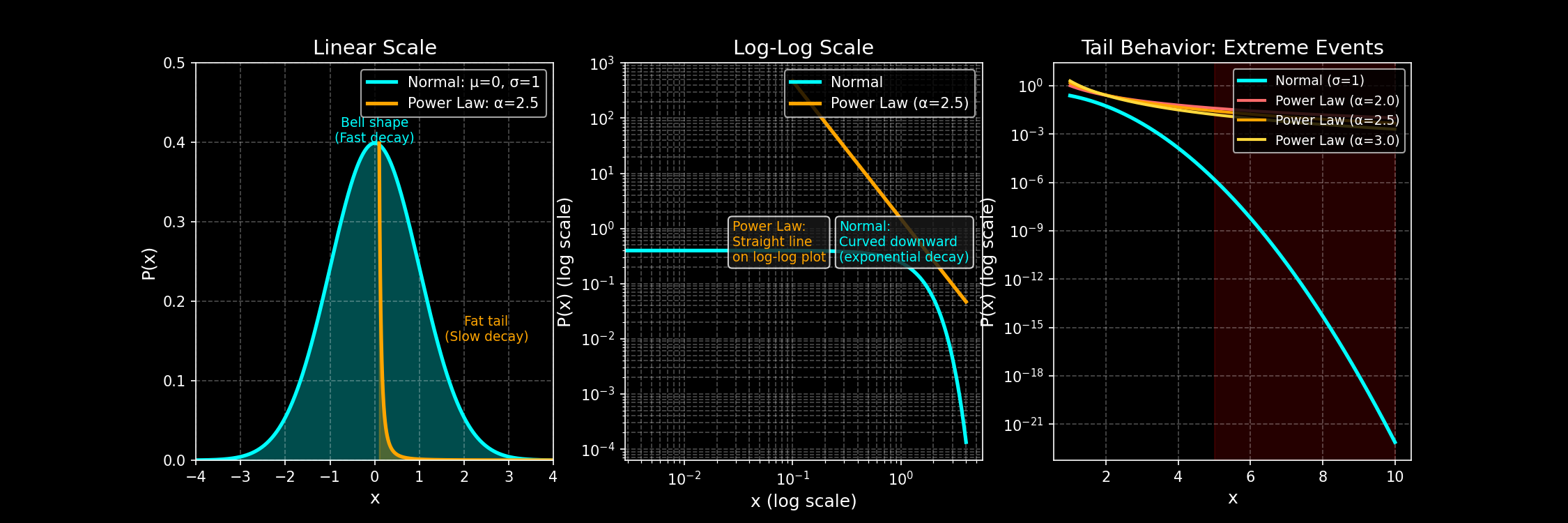
直观地看,正态分布的"尾巴"衰减得极快(指数衰减),而幂律分布的"尾巴"衰减得慢得多(多项式衰减)。这意味着在幂律分布中,极端事件虽然罕见,但绝非不可能。地震的震级分布、城市人口规模、财富分配、论文引用次数都呈现幂律特性——这些领域中,"黑天鹅"事件虽然稀少,却可能产生巨大影响。
幂律分布分析
回到沙堆模型,崩塌规模 s 的出现概率满足下面的关系:
$$P(s) = C s^{-\tau}$$
其中 τ 是幂律指数。为了从模拟数据估计 τ,我们采用最小二乘拟合。设有一组崩塌规模数据 ${s_i}$,首先统计每个规模值的出现频次,然后计算概率
$$P(s) = \frac{n(s)}{N}$$
其中 $n(s)$ 是规模为 s 的崩塌次数,N 是总崩塌次数。在对数坐标下进行线性回归
$$\min_{a,b} \sum_i (\log P(s_i) - a - b \log s_i)^2$$
拟合得到的斜率 $b = -\tau$。
完整代码如下所示:
import numpy as np
import matplotlib.pyplot as plt
from collections import Counter
# 参数设置 (与 06_sandpile_avalanche.py 一致)
GRID_SIZE = 40
THRESHOLD = 4
N_STEPS = 80000
# 高效沙堆模拟 (与 06_sandpile_avalanche.py 一致)
class Sandpile:
def __init__(self, size):
self.size = size
self.grid = np.zeros((size, size), dtype=np.int32)
self.total_grains = 0
self.avalanche_sizes = []
def add_grain(self):
self.grid[self.size // 2, self.size // 2] += 1
self.total_grains += 1
def topple_vectorized(self):
"""向量化崩塌 - 与 06_sandpile_avalanche.py 完全一致"""
avalanche = 0
while np.any(self.grid >= THRESHOLD):
topples = self.grid // THRESHOLD
self.grid -= topples * THRESHOLD
avalanche += np.sum(topples)
self.grid[1:, :] += topples[:-1, :]
self.grid[:-1, :] += topples[1:, :]
self.grid[:, 1:] += topples[:, :-1]
self.grid[:, :-1] += topples[:, 1:]
return avalanche
def step(self):
self.add_grain()
size = self.topple_vectorized()
if size > 0:
self.avalanche_sizes.append(size)
# 运行模拟
print(f"运行沙堆模拟 ({GRID_SIZE}x{GRID_SIZE}, {N_STEPS} 步)...")
sandpile = Sandpile(GRID_SIZE)
for i in range(N_STEPS):
sandpile.step()
if (i + 1) % 1000 == 0:
print(f" {i+1}/{N_STEPS}")
print(f"完成! 共 {sandpile.total_grains} 沙粒, {len(sandpile.avalanche_sizes)} 次崩塌")
# 幂律分布分析
sizes = np.array(sandpile.avalanche_sizes)
counts = Counter(sizes)
s_vals = np.array(sorted(counts.keys()))
p_vals = np.array([counts[s] for s in s_vals]) / len(sizes)
# 对数坐标下的线性拟合
log_s = np.log10(s_vals)
log_p = np.log10(p_vals)
# 只在有效范围内拟合 (避免尾部噪声)
valid = (p_vals > 1e-4) & (s_vals > 1) & (s_vals < np.percentile(s_vals, 90))
slope, intercept = np.polyfit(log_s[valid], log_p[valid], 1)
tau = -slope
print(f"\n幂律指数 τ = {tau:.3f}")
# 可视化
plt.style.use('dark_background')
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
# 左图: 崩塌规模分布 (双对数)
ax1 = axes[0]
ax1.scatter(s_vals, p_vals, s=15, alpha=0.7, color='#66c2e0', label='Data')
fit_line = 10**(intercept + slope * log_s)
ax1.plot(s_vals, fit_line, 'r-', lw=2, label=f'Power law fit: τ = {tau:.2f}')
ax1.set_xscale('log')
ax1.set_yscale('log')
ax1.set_xlabel('Avalanche Size (s)', fontsize=12)
ax1.set_ylabel('Probability P(s)', fontsize=12)
ax1.set_title('Avalanche Size Distribution', fontsize=14)
ax1.legend(loc='upper right', fontsize=10)
ax1.grid(True, alpha=0.3, ls='--')
ax1.set_xlim(0.5, max(s_vals) * 2)
# 右图: 累积分布
ax2 = axes[1]
sorted_sizes = np.sort(sizes)
ccdf = 1 - np.arange(len(sorted_sizes)) / len(sorted_sizes)
ax2.plot(sorted_sizes, ccdf, color='#38a6d6', lw=1.5, label='CCDF')
ax2.set_xscale('log')
ax2.set_yscale('log')
ax2.set_xlabel('Avalanche Size (s)', fontsize=12)
ax2.set_ylabel('P(S > s)', fontsize=12)
ax2.set_title('Complementary Cumulative Distribution', fontsize=14)
ax2.legend(loc='upper right', fontsize=10)
ax2.grid(True, alpha=0.3, ls='--')
# 添加统计信息
stats_text = (f"Total steps: {N_STEPS}\n"
f"Total avalanches: {len(sizes)}\n"
f"Mean size: {np.mean(sizes):.1f}\n"
f"Max size: {np.max(sizes)}\n"
f"Power law exponent: τ = {tau:.2f}")
ax2.text(0.95, 0.95, stats_text, transform=ax2.transAxes, fontsize=10,
verticalalignment='top', horizontalalignment='right',
bbox=dict(boxstyle='round', facecolor='#1a1a1a', alpha=0.8),
family='monospace')
plt.tight_layout()
plt.savefig('../images/06_power_law_distribution.png', dpi=150,
facecolor='black', edgecolor='none')
print("\n图片已保存: images/06_power_law_distribution.png")
plt.show()
上述代码运行后的效果如下图所示:
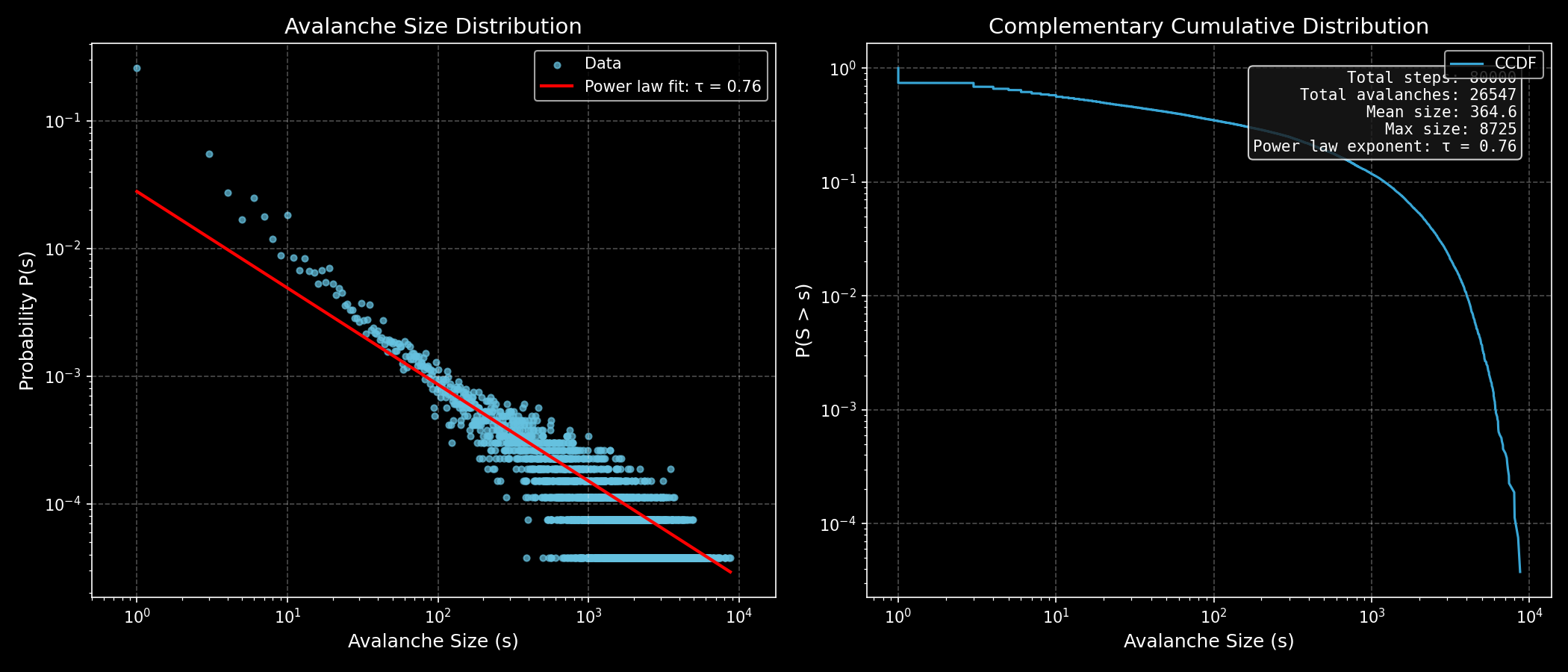
拟合得到的幂律指数约为 τ ≈ 0.756,这意味着小崩塌占据了绝大多数,但大崩塌虽然罕见,却并非不可能发生。正是这种"无特征尺度"的分布,使得沙堆模型能够解释地震震级分布、森林火灾面积分布等自然现象。值得注意的是,τ 的精确值会受网格尺寸、模拟步数等因素影响,但其存在性本身就是自组织临界性的关键证据。
总结
沙堆模型用最简单的规则——超过四粒就崩塌——展示了复杂系统最深刻的涌现行为。系统自发演化到临界状态,无需任何外部调节。小事件频繁发生,大事件偶尔出现,两者遵循相同的统计规律。这个模型深刻地改变了我们对复杂系统的理解。临界性可以是内禀的,而非外部强加的。沙堆模型也因此成为复杂系统科学中最经典的范例之一。
参考文献
[1] Bak, P., Tang, C., & Wiesenfeld, K. (1987). Self-organized criticality: An explanation of the 1/f noise. Physical Review Letters, 59(4), 381.
[2] Dhar, D. (1990). Self-organized critical state of sandpile automaton models. Physical Review Letters, 64(14), 1613.
 CycleUser
CycleUser