CycleUser

本系列受到 Allen B. Downey 的《Modeling and Simulation in Python》的启发，旨在通过 Python 编程语言，帮助新手同学来探索数学建模的基础内容。

什么是数学建模？

数学建模（Mathematical Modeling） 是用数学语言描述现实世界的过程。

想象一下，你想要在调整快门速度拍下球场上的运动员，或者根据云图预测明天的天气，又或者计算一枚火箭飞向火星的轨迹。这些现实问题往往充满了不确定性和复杂的细节。

数学建模就是把这些复杂的现实问题，通过假设和简化，翻译成数学公式或方程。一旦问题变成了数学题，我们就可以利用强大的数学工具（如微积分、线性代数、概率论）来求解。最后，我们将求得的数学答案再翻译回现实世界，看看它是否能解释现象或预测未来。

简单来说，数学建模就是：现实问题 $\rightarrow$ 数学模型 $\rightarrow$ 求解 $\rightarrow$ 解释与验证 的循环过程。

为何选用 Python？

在众多的编程语言中，Python 已经成为数学建模、数据科学和人工智能领域的首选语言。原因主要有以下几点：

简洁易读：Python 的语法非常简单，学起来比较快，阅读也方便，因为代码结构清晰。这意味着你可以把更多的精力放在“如何建立模型”上，而不是纠结于复杂的语法细节。
强大生态：Python 拥有海量的方库（Libraries）。无论是解微分方程、处理数据，还是绘制图表，都有现成的工具可用。也就是说，只要你有了思路，就可以调用工具来实现，而不用自己重新造轮子。
开源跨平台：Python 是免费且开源的，可以在 Windows、Mac 和 Linux 上流畅运行，你和队友的电脑硬件软件都不一样也不用担心，Python的代码都能运行。
社区支持：全球有无数的开发者在使用 Python，当你遇到问题时，很容易在网上找到解决方案。另外现在的AI工具，在训练的过程中，Python的代码规模可能是最多的，所以模型对Python的支持也会更加强大。

新手上路：安装与入门

如果你是第一次接触 Python，或者需要在一个新的环境中配置开发环境，以下资源可能将对你有帮助：

Windows 系统标准安装指南 如果你使用的是个人电脑，推荐使用 Miniconda 来管理 Python 环境。它轻量且易于管理，能有效避免环境冲突。
- Windows 系统下从清华大学 TUNA 镜像安装 Miniconda3 完整指南
便携版/绿化安装指南（U盘/公用机房适用） 如果你需要在学校机房、网吧等公用电脑上运行代码，或者希望把 Python 装在 U 盘里随身携带，可以使用“嵌入式版本”制作一个“绿色版” Python，即插即用，无需管理员权限。
- 打造绿色便携 Python：初步理解嵌入式 Python 与路径机制
Python 基础语法速成 在开始建模之前，你需要掌握最基本的 Python 语法（变量、循环、函数等）。这里有一份 5 分钟的快速入门指南，适合新手快速热身。
- Python 基础语法 5 分钟入门

库名称 (Library)	简介 (Description)	核心功能与典型用途
NumPy	Python 科学计算的基础包	数组与矩阵运算。提供高性能的多维数组对象（ndarray），用于线性代数、傅里叶变换和随机数生成。它是几乎所有其他科学计算库的基础。
Pandas	强大的数据分析和处理工具	表格数据处理。提供 DataFrame 数据结构，类似于 Excel 表格。用于数据的读取（CSV/Excel）、清洗、筛选、统计分析和时间序列处理。
Matplotlib	Python 最基础且强大的绘图库	数据可视化。可以生成出版质量的图形，如折线图、散点图、直方图、饼图等。虽然现在有很多新兴绘图库，但 Matplotlib 依然是根基。
SciPy	基于 NumPy 的高级科学计算库	高级数学算法。包含优化、积分、插值、特征值问题、信号处理、图像处理和常微分方程求解等模块。它是解决复杂数学问题的利器。
Pint	物理单位处理库	单位换算与管理。在物理建模中，确保单位（如米、秒、千克）的一致性至关重要。Pint 可以自动处理单位转换（如将米/秒转换为英里/时），避免量纲错误。

如何安装这些库？

推荐使用 Python 的包管理工具 pip 进行安装。由于官方源服务器在海外，下载速度可能较慢，强烈建议使用国内镜像源（如清华大学 TUNA 镜像）来加速安装。

1. 临时加速安装

你可以在安装命令后加上 -i 参数指定镜像源：

# 安装单个库
pip install numpy -i https://pypi.tuna.tsinghua.edu.cn/simple

# 一次性安装所有推荐库
pip install numpy pandas matplotlib scipy pint -i https://pypi.tuna.tsinghua.edu.cn/simple

如果下载了一份代码，其目录里面有 requirements.txt 文件，也可以直接使用 requirements.txt 文件进行批量安装：

pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple

2. 永久配置镜像（推荐）

为了避免每次都需要输入长长的镜像地址，你可以将清华源设置为默认源：

pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple

配置完成后，以后只需要运行 pip install 库名 即可自动享受高速下载。

如何使用这些库？炫技演示：蝴蝶效应

在 Python 代码中，我们通常使用 import 语句来加载这些库，并给它们起一个简短的别名（Alias），这已经成为了业界的约定俗成的规范：

import numpy as np              # 引入 NumPy，别名 np
import pandas as pd             # 引入 Pandas，别名 pd
import matplotlib.pyplot as plt # 引入 Matplotlib 的绘图模块，别名 plt
import scipy                    # 引入 SciPy
from pint import UnitRegistry   # 从 Pint 引入单位注册表

为了展示这些库如何协同工作，我们来编写一个稍微复杂一点的程序，模拟并绘制经典的混沌系统，著名的洛伦兹吸引子，即“蝴蝶效应”的起源。

1. 概念介绍

1963年，气象学家爱德华·洛伦兹（Edward Lorenz）在用计算机模拟大气对流时，发现了一个奇特的现象：初始数据的微小差异（例如 0.506 和 0.506127）会随着时间推移被指数级放大，最终导致完全不同的结果。这便是混沌理论的基石——对初始条件的敏感依赖性，也就导致了后来简化的文学说法“一只南美洲亚马逊河流域热带雨林中的蝴蝶，偶尔扇动几下翅膀，可以在两周以后引起美国德克萨斯州的一场龙卷风。”

2. 公式推导

洛伦兹简化了大气对流的纳维-斯托克斯方程，得到了一个看起来非常简洁的三维非线性微分方程组：

$$ \begin{cases} \frac{dx}{dt} = \sigma (y - x) \ \frac{dy}{dt} = x (\rho - z) - y \ \frac{dz}{dt} = xy - \beta z \end{cases} $$

3. 物理意义

在这个简化模型中，变量和参数都有具体的物理含义：

变量：
- $x$：流体对流的翻转速率。
- $y$：上升流与下降流之间的水平温差。
- $z$：垂直方向上的温度梯度偏差。
参数：
- $\sigma$ (Sigma)：普朗特数 (Prandtl number)，描述流体粘滞系数与热扩散系数的比值。
- $\rho$ (Rho)：瑞利数 (Rayleigh number)，描述流体受热程度。当 $\rho$ 超过临界值时，流体开始发生对流。
- $\beta$ (Beta)：与流体容器几何形状相关的常数。

当参数取经典值 $\sigma=10, \rho=28, \beta=8/3$ 时，系统不再收敛于任何一个稳定点，而是围绕着两个“吸引子”盘旋，形成类似蝴蝶双翼的轨迹，且永远不会重复自己的路径。

4. 代码实现

在这个示例中，我们将综合运用本书介绍的所有核心库。为了让结果更直观，我们将同时生成： 1. 静态 3D 散点图：使用颜色映射展示速度变化。 2. 动态 GIF 动画：展示洛伦兹吸引子的形成过程和混沌特性。

你可以直接运行 code/00_lorenz_attractor.py 文件：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from matplotlib.animation import FuncAnimation
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Line3DCollection
# 1. 定义数学模型
def lorenz_system(state, t, sigma=10.0, rho=28.0, beta=8.0/3.0):
    x, y, z = state
    return [sigma * (y - x), x * (rho - z) - y, x * y - beta * z]
# 2. 求解方程
initial_state = [1.0, 1.0, 1.0]
t = np.linspace(0, 50, 3000)
states = odeint(lorenz_system, initial_state, t)
df = pd.DataFrame(states, columns=['x', 'y', 'z'])
# 计算速度用于颜色映射
dx = np.diff(df['x'], prepend=df['x'].iloc[0])
dy = np.diff(df['y'], prepend=df['y'].iloc[0])
dz = np.diff(df['z'], prepend=df['z'].iloc[0])
df['velocity'] = np.sqrt(dx**2 + dy**2 + dz**2)
# 设置绘图风格
plt.style.use('dark_background')
# ==========================================
# Part A: 静态 3D 散点图（无边框优化）
fig_static = plt.figure(figsize=(10, 8), facecolor='black')
ax_static = fig_static.add_subplot(111, projection='3d')
ax_static.set_facecolor('black')
# 绘制轨迹 (改为使用 Line3DCollection 以获得清晰连续的线条)
points = np.array([df['x'], df['y'], df['z']]).T.reshape(-1, 1, 3)
segments = np.concatenate([points[:-1], points[1:]], axis=1)
# 创建彩色线条集合
# 使用 'cool' colormap (青色到洋红) 在黑色背景下对比度极佳
norm = plt.Normalize(df['velocity'].min(), df['velocity'].max())
lc = Line3DCollection(segments, cmap='cool', norm=norm)
lc.set_array(df['velocity'][:-1]) # 设置每段的颜色值
lc.set_linewidth(1.5)             # 增加线宽
lc.set_alpha(0.8)                 # 设置透明度
# 添加到绘图区
ax_static.add_collection(lc)
# 关键：Line3DCollection 不会自动调整坐标轴范围，需手动设置
ax_static.set_xlim(df['x'].min(), df['x'].max())
ax_static.set_ylim(df['y'].min(), df['y'].max())
ax_static.set_zlim(df['z'].min(), df['z'].max())
# 添加嵌入式标题（避免外部标题导致边距）
ax_static.text2D(0.5, 0.96, 'The Lorenz Attractor (Static)', 
                transform=ax_static.transAxes,
                color='white', fontsize=18, ha='center', va='top',
                fontweight='bold')
# 关闭坐标轴与边框
ax_static.set_axis_off()
ax_static.grid(False)
ax_static.set_box_aspect([ub - lb for lb, ub in (getattr(ax_static, f'get_{a}lim')() for a in 'xyz')])
# 移除所有图形边距
plt.subplots_adjust(left=0, right=1, top=1, bottom=0)
# 保存：tight bbox + 零填充 + 黑色背景
plt.savefig('00_lorenz_attractor.png', 
            bbox_inches='tight', 
            pad_inches=0,
            dpi=150)
plt.close(fig_static)
# Part B: 动态 GIF 动画
fig_anim = plt.figure(figsize=(10, 8), facecolor='black')
ax_anim = fig_anim.add_subplot(111, projection='3d')
ax_anim.set_facecolor('black')
ax_anim.set_axis_off()
ax_anim.grid(False)
# 嵌入式标题（固定在视图内，避免裁剪）
ax_anim.text2D(0.5, 0.96, 'The Lorenz Attractor\nChaos in Motion', 
              transform=ax_anim.transAxes,
              color='white', fontsize=18, ha='center', va='top',
              fontweight='bold', linespacing=1.4)
# 设置坐标范围
x_min, x_max = df['x'].min(), df['x'].max()
y_min, y_max = df['y'].min(), df['y'].max()
z_min, z_max = df['z'].min(), df['z'].max()
ax_anim.set_xlim(x_min, x_max)
ax_anim.set_ylim(y_min, y_max)
ax_anim.set_zlim(z_min, z_max)
ax_anim.set_box_aspect([x_max-x_min, y_max-y_min, z_max-z_min])
# 初始化轨迹线与轨迹头
line, = ax_anim.plot([], [], [], lw=1.5, color='#ff1aff', alpha=0.9)
head, = ax_anim.plot([], [], [], 'o', color='white', markersize=5, alpha=0.9)
# 移除所有图形边距（关键：避免动画抖动）
plt.subplots_adjust(left=0, right=1, top=1, bottom=0)
# 动画更新函数
step = 8
def update(frame):
    idx = min(frame * step, len(df) - 1)
    line.set_data(df['x'].values[:idx], df['y'].values[:idx])
    line.set_3d_properties(df['z'].values[:idx])
    head.set_data([df['x'].iloc[idx]], [df['y'].iloc[idx]])
    head.set_3d_properties([df['z'].iloc[idx]])
    ax_anim.view_init(elev=20, azim=frame * 0.6)
    return line, head
frames = len(df) // step
ani = FuncAnimation(fig_anim, update, frames=frames, interval=20, blit=False)
# 保存动画：指定facecolor，不使用bbox_inches（避免帧间抖动）
ani.save('https://raw.githubusercontent.com/cycleuser/cycleuser.github.io/refs/heads/main/img/MathPython/00_lorenz_animation.gif', 
         writer='pillow', 
         fps=30,
         savefig_kwargs={'facecolor': 'black'})
plt.close(fig_anim)

5. 可视化结果

我们首先得到了一张精美的静态全景图，通过颜色的深浅（速度大小）可以直观感受到系统的动态特性。

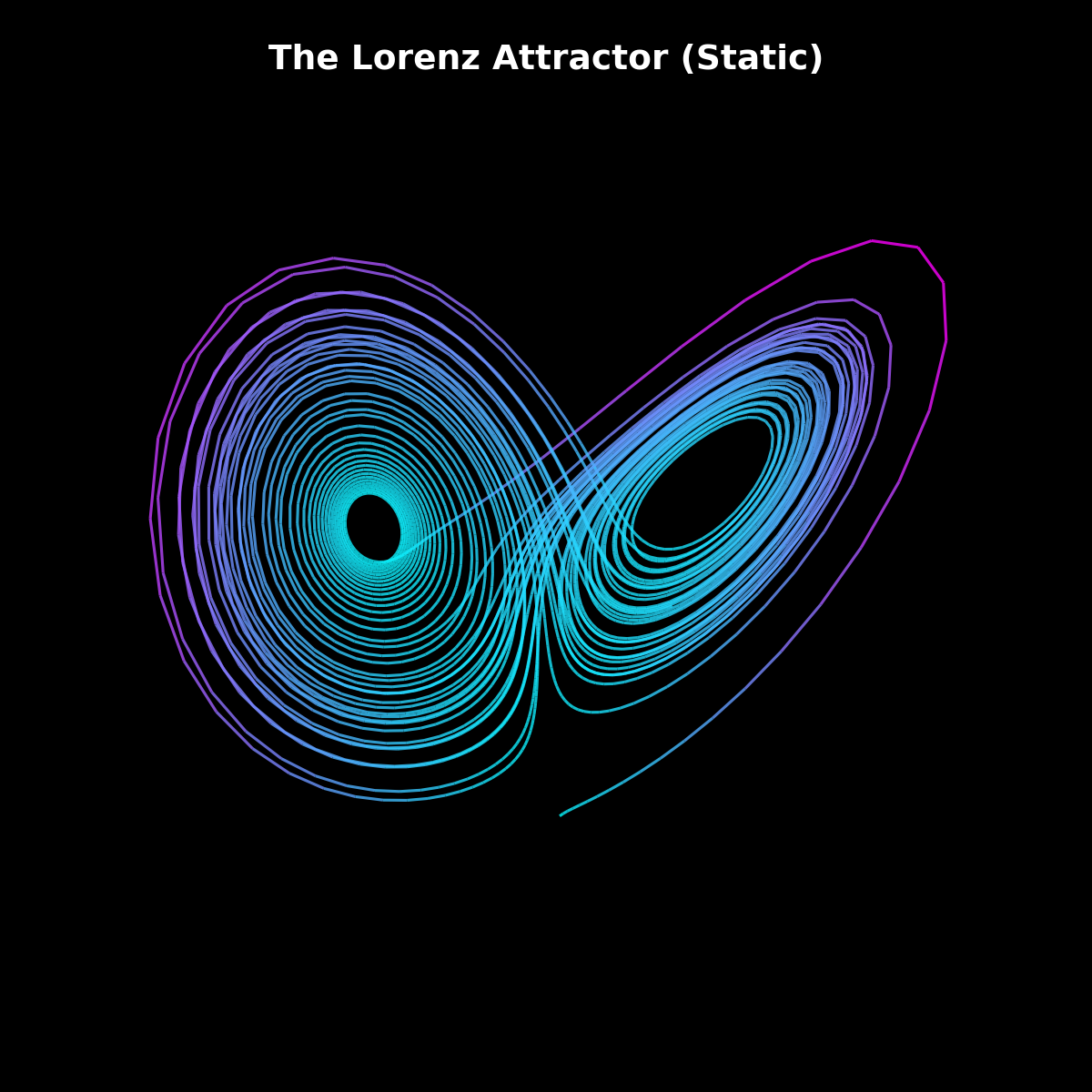
洛伦兹吸引子（静态）

而通过动态 GIF，可以更好地观察到系统是如何从一个初始点开始，逐渐演化出复杂的混沌结构的。配合动态旋转的视角，整个过程如同在深空中观察一只蝴蝶。

洛伦兹吸引子（动态）

总结

数学建模是连接现实与数学的桥梁，而 Python 则是我们搭建这座桥梁的现代化施工队。