本系列受到 Allen B. Downey 的《Modeling and Simulation in Python》的启发,旨在通过 Python 编程语言,帮助新手同学来探索数学建模的基础内容。
知识背景
仰望星空,行星的运行轨迹一直是人类最着迷的谜题之一。从托勒密的地心说,到哥白尼的日心说,再到牛顿的万有引力定律,我们一步步揭开了天体运动的规律。
在本章中,我们将不再局限于简单的数据拟合,而是直接从物理学的基本定律出发,构建一个简化的三体系统(Three-Body System)——太阳、地球和月球,并使用 Python 模拟它们在引力作用下的舞蹈。
概念介绍
要模拟天体运动,我们需要理解以下核心概念:
-
万有引力定律:宇宙中任何两个物体之间都存在引力。 $$F = G \frac{m_1 m_2}{r^2}$$ 其中 $G$ 是引力常数,$m$ 是质量,$r$ 是距离。
-
牛顿第二定律:力决定了物体的加速度。 $$F = ma \Rightarrow a = \frac{F}{m}$$
-
多体问题:当只有两个天体时(如地球和太阳),它们的轨道是完美的椭圆,这是开普勒定律告诉我们的。但一旦加入第三个天体(如月球),系统就变成了“三体问题”。虽然日地月系统的轨道相对稳定,但在数学上它是不可解析的,我们必须使用计算机进行数值模拟。
向量运算与物理建模
为了方便计算,我们使用向量(Vector)来描述位置、速度和力。
1. 状态定义
每个天体都有两个向量属性: * 位置向量 $\vec{p} = (x, y)$ * 速度向量 $\vec{v} = (v_x, v_y)$
2. 引力加速度
对于任意天体 A,它受到的来自天体 B 的引力加速度 $\vec{a}{AB}$ 方向指向 B,大小为: $$|\vec{a}$$ 向量形式为: $$\vec{a}_{AB} = \frac{G M_B}{|\vec{r}|^3} \vec{r}$$ 其中 $\vec{r} = \vec{p}_B - \vec{p}_A$ 是从 A 指向 B 的位移向量。}| = \frac{G M_B}{r^2
如果系统中有多个天体,天体 A 受到的总加速度就是所有其他天体对它施加的加速度的向量和。
3. 数值积分
知道了加速度,我们就可以通过迭代来更新速度和位置。这里我们使用简单的欧拉-克罗默方法(Euler-Cromer Method),它比标准的欧拉法更能保持能量守恒,适合轨道模拟。
在每个微小的时间步 $\Delta t$ 中: 1. 计算加速度:$\vec{a}{new} = \sum \vec{a}$ 2. 更新速度:$\vec{v}{new} = \vec{v}} + \vec{a{new} \times \Delta t$ 3. 更新位置:$\vec{p}} = \vec{p{old} + \vec{v} \times \Delta t$
代码实现与可视化
为了展示这一过程,我们编写了一个 Python 脚本,模拟一个真实的日地月系统。
由于日地距离(1.5亿公里)远大于地月距离(38万公里),为了让它们能在一个画面中清晰展示,我们采用了一种相对坐标缩放(Log-Like Scaling)的技巧: 1. 日地距离:按比例缩小,使其能放入屏幕。 2. 地月距离:在真实比例的基础上放大 50 倍。
这种处理方式虽然扭曲了真实的空间比例,但能让我们直观地看到月球绕地运动与地球绕日运动的耦合关系。
核心代码
你可以直接运行 code/03_solar_system.py 查看完整效果。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# 真实物理参数 (SI 单位制)
G = 6.67430e-11
M_SUN = 1.989e30
M_EARTH = 5.972e24
M_MOON = 7.348e22
AU = 1.496e11
DIST_MOON = 3.844e8
V_EARTH_MEAN = 29780
V_MOON_MEAN = 1022
# 初始化状态
pos_sun = np.array([0.0, 0.0], dtype=np.float64)
vel_sun = np.array([0.0, 0.0], dtype=np.float64)
pos_earth = np.array([AU, 0.0], dtype=np.float64)
vel_earth = np.array([0.0, V_EARTH_MEAN], dtype=np.float64)
pos_moon = np.array([AU + DIST_MOON, 0.0], dtype=np.float64)
vel_moon = np.array([0.0, V_EARTH_MEAN + V_MOON_MEAN], dtype=np.float64)
positions = np.array([pos_sun, pos_earth, pos_moon])
velocities = np.array([vel_sun, vel_earth, vel_moon])
masses = np.array([M_SUN, M_EARTH, M_MOON])
# 模拟设置
dt = 3600 * 6 # 6小时
total_duration = 365 * 24 * 3600
steps = int(total_duration / dt)
traj = np.zeros((steps, 3, 2))
# 数值积分 (Velocity Verlet)
def get_accelerations(pos, m):
n = pos.shape[0]
acc = np.zeros_like(pos)
for i in range(n):
for j in range(n):
if i != j:
r_vec = pos[j] - pos[i]
r_mag = np.linalg.norm(r_vec)
acc[i] += G * m[j] * r_vec / (r_mag**3)
return acc
acc = get_accelerations(positions, masses)
for i in range(steps):
traj[i] = positions
velocities += 0.5 * acc * dt
positions += velocities * dt
new_acc = get_accelerations(positions, masses)
velocities += 0.5 * new_acc * dt
acc = new_acc
# 对数极坐标变换 (Log-Polar Transform)
def transform_to_log_polar(pos):
"""
将笛卡尔坐标转换为对数极坐标,再映射回直角坐标以便绘图。
r_new = log10(r + 1)
"""
x, y = pos
r = np.sqrt(x**2 + y**2)
theta = np.arctan2(y, x)
return x, y # 占位
SCALE_EARTH = 1.0 / AU * 10.0 # 把 1 AU 映射为 10 个单位
SCALE_MOON_REL = 50.0 # 把地月距离放大 50 倍以便可见
traj_vis = np.zeros_like(traj)
# 太阳固定在原点 (或者稍微抖动,这里忽略抖动)
traj_vis[:, 0, :] = 0.0
# 地球按比例缩放
traj_vis[:, 1, :] = traj[:, 1, :] * SCALE_EARTH
# 月球:先计算相对地球的矢量,放大后再加回地球的缩放位置
rel_moon = traj[:, 2, :] - traj[:, 1, :]
# 为了让月球轨道更清楚,我们将相对距离归一化后,赋予一个固定的视觉距离,或者乘以一个大系数
# 这里直接乘以大系数,保持椭圆特征
traj_vis[:, 2, :] = traj_vis[:, 1, :] + rel_moon * SCALE_EARTH * SCALE_MOON_REL
# 可视化
plt.style.use('dark_background')
fig, ax = plt.subplots(figsize=(10, 10))
ax.set_aspect('equal')
ax.set_xlim(-12, 12)
ax.set_ylim(-12, 12)
ax.axis('off')
# 轨道线
earth_orbit, = ax.plot([], [], '--', color='#3498db', lw=0.5, alpha=0.3) # 地球轨道
# 星体
sun, = ax.plot([0], [0], 'o', color='#f39c12', markersize=100, label='Sun')
earth, = ax.plot([], [], 'o', color='#3498db', markersize=18, label='Earth')
moon, = ax.plot([], [], 'o', color='#ecf0f1', markersize=9, label='Moon')
trail_moon, = ax.plot([], [], '-', color='#ecf0f1', lw=1, alpha=0.5)
trail_earth, = ax.plot([], [], '-', color='#3498db', lw=1.5, alpha=0.4) # 地球轨迹
ax.legend(loc='upper right', frameon=False)
ax.set_title("Solar System\n(Log-Like Visualization)\nMoon-Earth\ndistance magnified 50x", color='white')
def update(frame):
idx = frame * 10
if idx >= steps: idx = steps - 1
p_e = traj_vis[idx, 1]
p_m = traj_vis[idx, 2]
earth.set_data([p_e[0]], [p_e[1]])
moon.set_data([p_m[0]], [p_m[1]])
# 地球轨迹
tail = 200
start = max(0, idx - tail)
trail_earth.set_data(traj_vis[start:idx, 1, 0], traj_vis[start:idx, 1, 1])
# 月球轨迹 (相对于地球的螺旋)
trail_moon.set_data(traj_vis[start:idx, 2, 0], traj_vis[start:idx, 2, 1])
# 绘制完整的地球轨道作为背景参考
earth_orbit.set_data(traj_vis[:idx, 1, 0], traj_vis[:idx, 1, 1])
return earth, moon, trail_moon, trail_earth, earth_orbit
frames = steps // 10
ani = FuncAnimation(fig, update, frames=frames, interval=20, blit=True)
ani.save('../images/03_solar_system.gif', writer='pillow', fps=30)
print("Animation saved.")
可视化结果
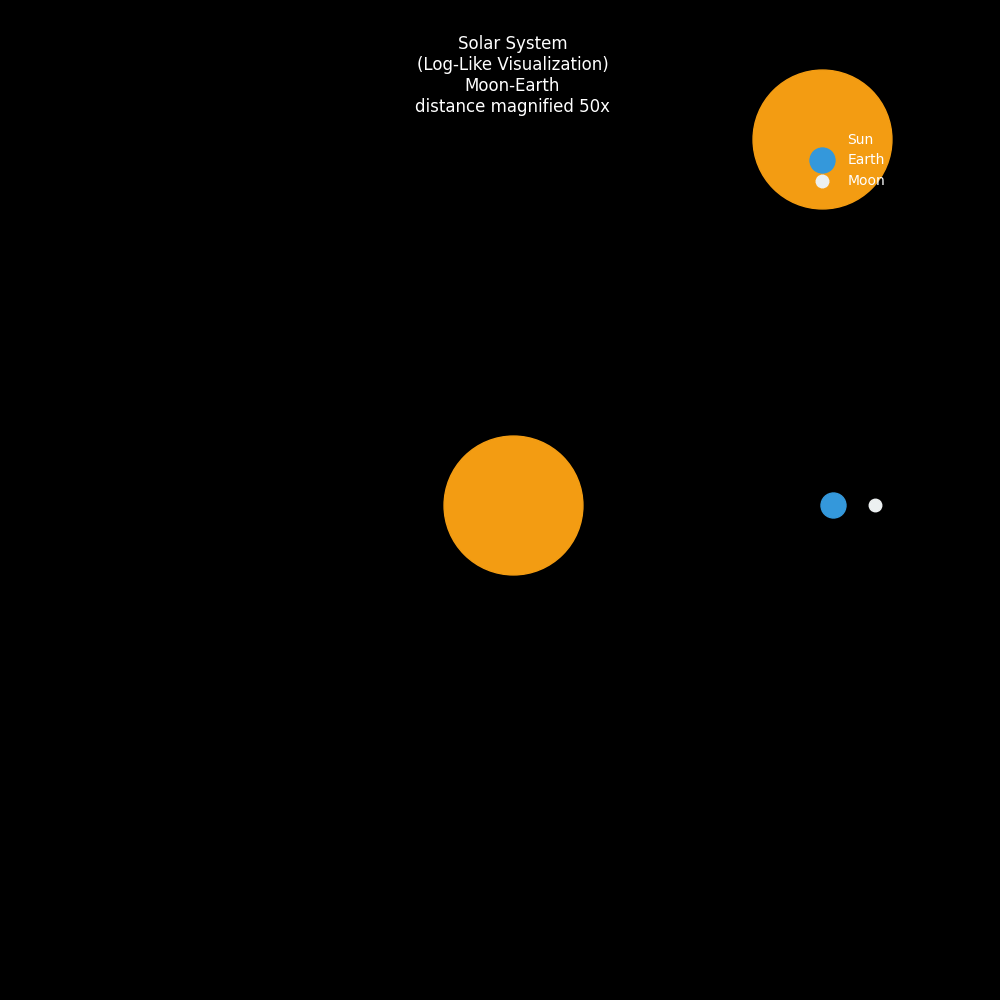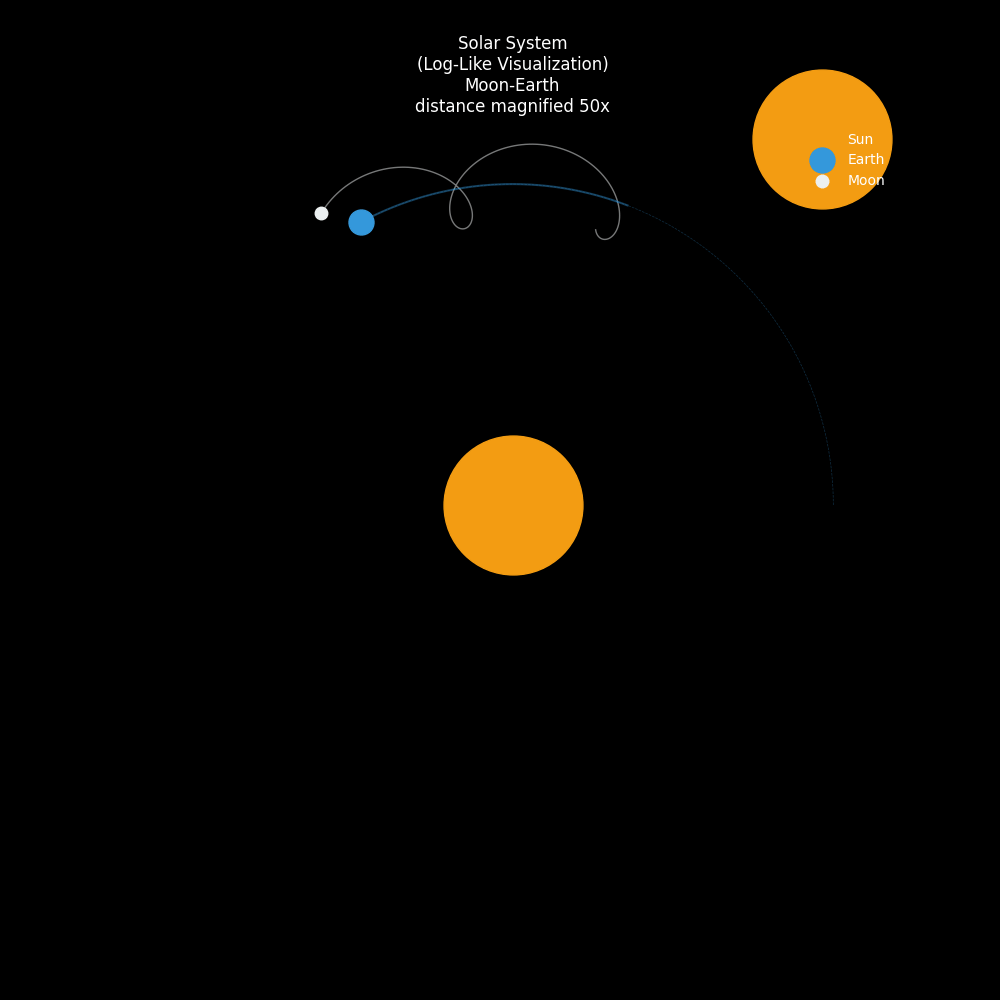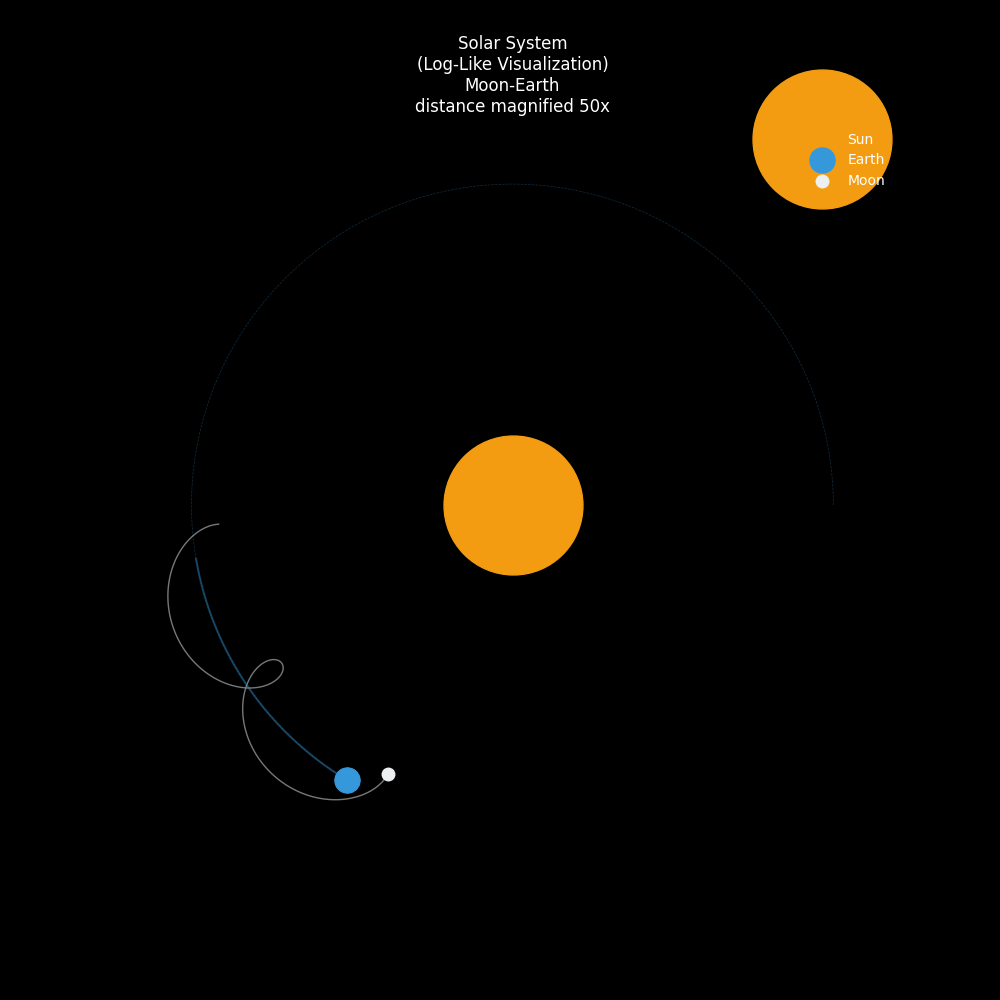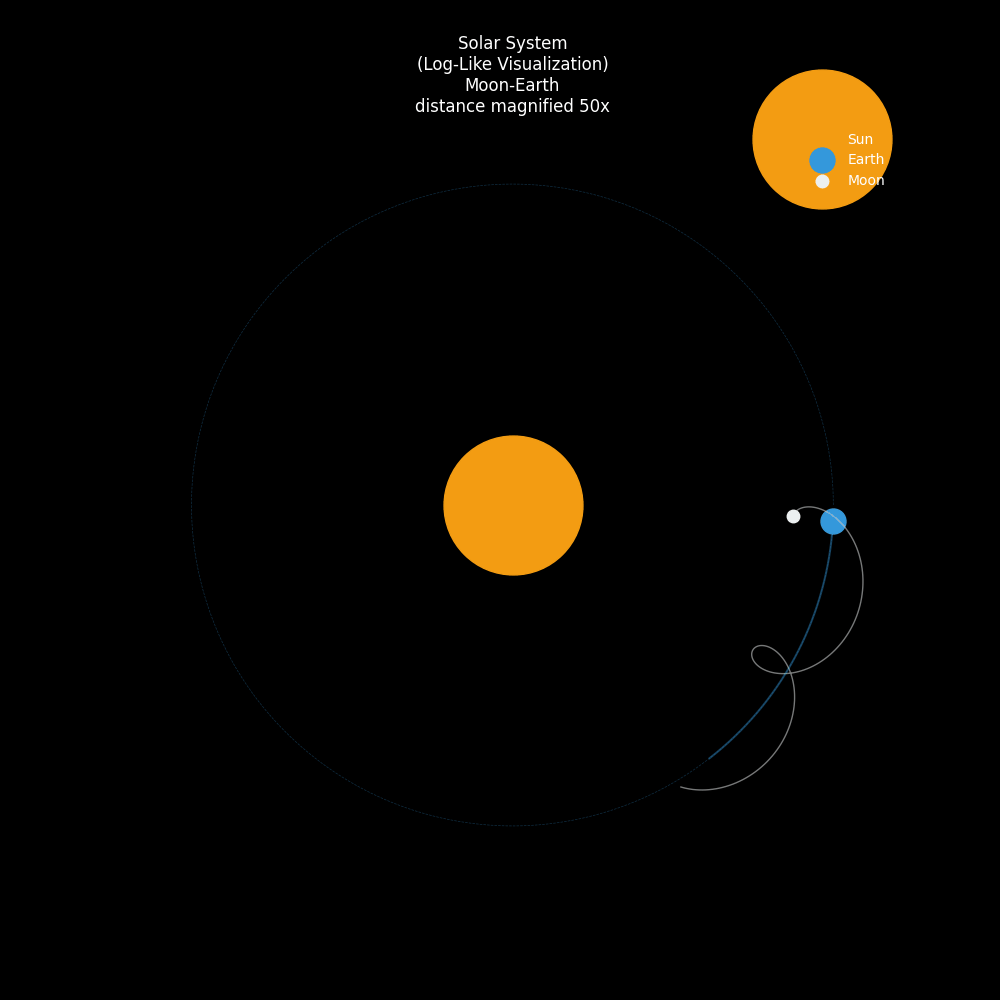
下面的动画展示了在一个统一视图下的三体运动:
- 太阳(黄色):位于中心。
- 地球(蓝色):沿着圆形轨道绕日运行。
- 月球(白色):围绕地球旋转,同时跟随地球绕日,其轨迹呈现出一种美丽的外摆线(Epitrochoid)特征,就像一个在弹簧上跳舞的精灵。
拓展:三体问题的混沌之舞
虽然日地月系统在短时间内相对稳定,但在一般情况下,三个质量相近的天体在引力作用下的运动是极度混沌(Chaotic)的。这意味着初始条件的微小差异会导致轨道在后期发生巨大的、不可预测的变化。
然而,在混沌的海洋中,数学家们也发现了一些奇迹般的周期解。最著名的就是 Chenciner 和 Montgomery 在 2000 年发现的 "Figure-8"(8字形)轨道。在这个解中,三个天体在一条 8 字形的轨道上互相追逐,周而复始。
核心代码
我们编写了一个额外的脚本 code/03_three_body_chaos.py 来模拟这个迷人的现象,完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# 混沌三体系统参数
# 采用经典的 "Figure-8" 轨道(由 Moore 发现,Chenciner & Montgomery 证明)
# 这是一个稳定的周期解,但对初始条件非常敏感(混沌边缘)
G = 1.0
m1 = m2 = m3 = 1.0
# 初始条件 (Chenciner & Montgomery, 2000)
p1 = 0.3471168124
p2 = 0.5327249448
p_init = np.array([
[0.97000436, -0.24308753], # Body 1
[-0.97000436, 0.24308753], # Body 2
[0.0, 0.0] # Body 3
])
v_init = np.array([
[p1, p2], # Body 1
[p1, p2], # Body 2
[-2*p1, -2*p2] # Body 3
])
positions = p_init.copy()
velocities = v_init.copy()
masses = np.array([m1, m2, m3])
# 数值积分 (Velocity Verlet)
dt = 0.005
steps = 2000
traj = np.zeros((steps, 3, 2))
def get_acc(pos, m):
n = pos.shape[0]
acc = np.zeros_like(pos)
for i in range(n):
for j in range(n):
if i != j:
r_vec = pos[j] - pos[i]
r_mag = np.linalg.norm(r_vec) + 1e-9 # 避免除零
acc[i] += G * m[j] * r_vec / (r_mag**3)
return acc
acc = get_acc(positions, masses)
for i in range(steps):
traj[i] = positions
velocities += 0.5 * acc * dt
positions += velocities * dt
new_acc = get_acc(positions, masses)
velocities += 0.5 * new_acc * dt
acc = new_acc
# 动态可视化 (拖尾效果)
plt.style.use('dark_background')
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_aspect('equal')
ax.set_xlim(-2, 2)
ax.set_ylim(-1.5, 1.5)
ax.axis('off')
# 颜色
colors = ['#e74c3c', '#2ecc71', '#3498db'] # 红绿蓝
bodies = [ax.plot([], [], 'o', color=c, markersize=18)[0] for c in colors]
trails = [ax.plot([], [], '-', color=c, lw=1.5, alpha=0.6)[0] for c in colors]
ax.set_title("Three-Body Problem", color='white', fontsize=16)
def update(frame):
# 加快动画播放速度
idx = frame * 4
if idx >= steps: idx = steps - 1
# 拖尾长度
tail = 300
start = max(0, idx - tail)
for i in range(3):
# 更新物体位置
p = traj[idx, i]
bodies[i].set_data([p[0]], [p[1]])
# 更新拖尾
t = traj[start:idx, i]
trails[i].set_data(t[:, 0], t[:, 1])
return bodies + trails
frames = steps // 4
ani = FuncAnimation(fig, update, frames=frames, interval=20, blit=True)
ani.save('../images/03_three_body_chaos.gif', writer='pillow', fps=30)
print("Chaos animation saved to ../images/03_three_body_chaos.gif")
可视化结果
三个天体在引力的牵引下,竟然地在太空中画出了一个类似“8”字。

总结
通过这个模型,我们不仅复现了我们熟悉的宇宙图景,更重要的是,我们验证了简单的物理定律(万有引力)足以涌现出复杂的系统行为。月球并没有被专门设定要绕地球转,它的运动完全是它在每一个瞬间受到的合力自然导致的结果。这就是物理计算的魅力所在。
 CycleUser
CycleUser