CycleUser

本系列受到 Allen B. Downey 的《Modeling and Simulation in Python》的启发，旨在通过 Python 编程语言，帮助新手同学来探索数学建模的基础内容。

知识背景

1952年，计算机科学之父艾伦·图灵（Alan Turing）在《英国皇家学会哲学汇刊》上发表了一篇题为《形态发生的化学基础》的论文。这篇论文提出了一个看似违反直觉的观点：扩散——这个本应让物质分布趋于均匀的过程——竟然能够产生有序的空间图案。

图灵当时关注的核心问题是：一个最初完全均匀的受精卵，如何能够发育成具有复杂空间结构的生物体？头在哪里长、尾巴在哪里长、条纹和斑点如何形成——这些问题困扰着生物学家多年。图灵用数学证明，仅仅依靠化学物质的反应和扩散，就足以让均匀的系统自发产生图案。

这个发现的意义远超生物学。它揭示了自然界中一个普遍的原理：简单的局部相互作用，可以涌现出复杂的全局结构。

概念介绍

本节从方程本身出发来描述图灵的形态发生机制, 并且逐步对应到下面给出的 Python 实现。

设 $U(x,y,t)$ 和 $V(x,y,t)$ 分别是二维空间中位置 $(x,y)$、时间 $t$ 处两种化学物质的浓度。一般的双组分反应–扩散系统可以写成

$$ \frac{\partial U}{\partial t} = f(U,V) + D_U \nabla^2 U, \qquad \frac{\partial V}{\partial t} = g(U,V) + D_V \nabla^2 V. $$

这里 $f,g$ 是局部反应项, $D_U, D_V \ge 0$ 是扩散系数, $\nabla^2$ 是二维拉普拉斯算子

$$ \nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}, $$

描述的是浓度沿空间坐标的扩散。没有扩散时($D_U=D_V=0$), 每个空间点只按局部反应 $f,g$ 演化; 引入扩散之后, 空间不同位置之间通过 $\nabla^2$ 相互耦合, 有可能出现由扩散触发的不稳定性。

在本文中我们采用 Gray–Scott 模型作为具体例子。该模型通过适当无量纲化之后, 其局部反应项取为

$$ f(U,V) = -U V^2 + F(1-U), \qquad g(U,V) = U V^2 - (F+k)V, $$

从而得到反应–扩散方程

$$ \frac{\partial U}{\partial t} = D_U \nabla^2 U -U V^2 + F(1-U), $$

$$ \frac{\partial V}{\partial t} = D_V \nabla^2 V + U V^2 - (F+k)V. $$

其中 $F$ 是外界持续补充 $U$ 的速率(feed rate), $k$ 是 $V$ 的附加消耗速率(kill rate)。非线性项 $U V^2$ 体现了 $V$ 的自催化作用: 一旦某处 $V$ 略有增加, 该项会加速 $V$ 的生成, 同时消耗 $U$。这类正反馈配合扩散, 就可能打破原本的空间均匀状态, 产生稳定的空间图案。

Gray–Scott 模型与连续方程

在忽略扩散时(即 $D_U=D_V=0$), 上述方程在每个空间点退化为一组常微分方程

$$ \frac{\mathrm d U}{\mathrm d t} = -U V^2 + F(1-U), \qquad \frac{\mathrm d V}{\mathrm d t} = U V^2 - (F+k)V. $$

平衡态满足右端为零。令

$$ \frac{\mathrm d U}{\mathrm d t} = 0, \qquad \frac{\mathrm d V}{\mathrm d t} = 0, $$

得到代数方程组

$$ -U V^2 + F(1-U) = 0, \qquad U V^2 - (F+k)V = 0. $$

第二个方程可化为

$$ V\,(U V - F - k) = 0, $$

因此存在两类均匀平衡解:

$V = 0$ 时, 由第一个方程得 $F(1-U)=0$, 即 $(U,V)=(1,0)$, 这是系统最自然的均匀基态;
$V > 0$ 时, 必有 $U V = F + k$, 即 $U = \dfrac{F+k}{V}$。代回第一个方程

$$ -U V^2 + F(1-U) = 0 $$

得到

$$ F = U\,(F+V^2) = \frac{F+k}{V}(F+V^2), $$

即

$$ F V = (F+k)(F+V^2). $$

对于给定的 $(F,k)$, 上式是关于 $V$ 的三次代数方程, 一般需要数值求解。不同解对应不同的均匀平衡, 它们的稳定性则由后文“数学视角”部分的线性稳定性分析给出。Gray–Scott 相图[4,5] 正是以这些均匀平衡为出发点, 研究在哪些参数区域会出现由扩散驱动的空间结构。

需要强调的是, 经典的“激活–抑制”图灵模型通常假设抑制组分扩散更快; 而在 Gray–Scott 模型的常用参数下, $U$ 更像是被持续补充的基质, $V$ 扮演自催化组分的角色, 扩散系数也不一定满足简单的大小关系。尽管如此, 其数学结构仍然属于反应–扩散系统, 能够产生典型的扩散驱动不稳定性。

数值离散与代码实现

为了在计算机上模拟上述偏微分方程, 我们将时间和空间都离散化。设空间用正方形网格近似, 网格步长为 $h$, 用 $U_{i,j}(t)$ 表示格点 $(i,j)$ 处的浓度。二维拉普拉斯算子在 $(i,j)$ 点的标准五点差分近似为

$$ \nabla^2 U(x,y,t)\big|{(x_i,y_j)} \approx \frac{U. $$} + U_{i-1,j} + U_{i,j+1} + U_{i,j-1} - 4 U_{i,j}}{h^2

在代码中我们取 $h=1$, 并将 $1/h^2$ 吸收到 $D_U,D_V$ 中, 因此离散拉普拉斯可以简写为

$$ \Delta_h U_{i,j} = U_{i+1,j} + U_{i-1,j} + U_{i,j+1} + U_{i,j-1} - 4 U_{i,j}. $$

turing 模拟器中的 laplacian 方法

对应的正是上述 $\Delta_h$, 通过 np.roll 在四个方向上平移数组并求和, 从而实现周期边界条件(左边界与右边界、上边界与下边界首尾相接)。

对时间离散, 记时间步长为 $\Delta t$, 用上标 $n$ 表示第 $n$ 个时间层, 采用显式欧拉法

$$ U_{i,j}^{n+1} = U_{i,j}^{n} + \Delta t\, \Big[ D_U \Delta_h U_{i,j}^{n} -U_{i,j}^{n} (V_{i,j}^{n})^2 + F (1 -U_{i,j}^{n}) \Big], $$

$$ V_{i,j}^{n+1} = V_{i,j}^{n} + \Delta t\, \Big[ D_V \Delta_h V_{i,j}^{n} + U_{i,j}^{n} (V_{i,j}^{n})^2 - (F+k) V_{i,j}^{n} \Big]. $$

与代码逐项对照可以看到:

uvv = self.U * self.V * self.V 对应非线性反应项 $U V^2$;
self.du * self.laplacian(self.U) 和 self.dv * self.laplacian(self.V) 分别实现 $D_U \Delta_h U$ 和 $D_V \Delta_h V$;
self.feed * (1 - self.U) 实现补充项 $F(1-U)$;
(self.feed + self.kill) * self.V 对应消耗项 $(F+k)V$;
self.U += dt * dU, self.V += dt * dV 正是显式欧拉格式 $u^{n+1} = u^n + \Delta t\,f(u^n)$ 的离散写法。

在三段代码(斑点、条纹、迷宫)中, 所有这些数值结构完全相同, 只有参数 $(D_U,D_V,F,k)$、网格大小和初始扰动方式不同, 图案类型的差异正是由这些参数和初值共同决定的。

参数的影响

在给定的数值格式下, Gray–Scott 模型的主要控制参数是 $F$ 和 $k$, 扩散系数 $D_U,D_V$ 则决定图案的空间尺度和平滑程度。先考虑不含扩散的均匀系统, 即令 $D_U=D_V=0$。此时的平衡态由

$$ -U V^2 + F(1-U) = 0, \qquad U V^2 - (F+k)V = 0 $$

确定。上文已经给出了 $(U,V)=(1,0)$ 以及由方程 $F V = (F+k)(F+V^2)$ 确定的非平凡平衡。在线性稳定性分析中, 我们先判断这些均匀平衡在无扩散情形下是否稳定, 然后再考察加入扩散后某些空间模式是否会获得正的增长率, 这正是“图灵不稳定性”的数学表述(见后文“数学视角”部分)。

从物理直觉出发可以这样理解参数的作用:

$F$ (feed rate) 决定外界向系统持续注入基质 $U$ 的速率。$F$ 较小时, 系统更接近 $(U,V)=(1,0)$ 的均匀状态, 只有局部扰动才能维持少量活跃区域; 适当增大 $F$ 会使 $U$ 和 $V$ 的平衡浓度提高, 非线性反应 $U V^2$ 更频繁地被触发, 从而产生更密集的结构;
$k$ (kill rate) 决定 $V$ 的额外衰减强度。$k$ 较大时, $V$ 很难在局部长期维持高浓度, 形成的结构更细长、易于延伸成条带; $k$ 较小时, $V$ 的衰减减弱, 活跃区域可以在局部稳定存在, 更容易形成孤立斑点或互相连接成复杂网络。

在本文的三组数值实验中, 参数取值为

图案类型	$F$ (feed)	$k$ (kill)	$D_U$	$D_V$	特征
斑点	0.062	0.061	0.16	0.08	局域集中, 间隔均匀
条纹	0.026	0.052	0.14	0.06	细长条带, 近似平行
迷宫	0.039	0.058	0.16	0.08	互相连接, 拓扑复杂

这些点都位于 Gray–Scott 相图[4,5] 中的典型区域: 在 $(F,k)$ 平面上缓慢移动会引发从孤立斑点到规则条纹再到迷宫状网络的连续形态转变。数值实验提供了这些理论结论的直观可视化, 也为后文的稳定性分析给出了具体的参数背景。

完整代码

下面的三分代码分别对斑点、条纹、迷宫这三种图案的形成过程进行可视化模拟：

斑点图案

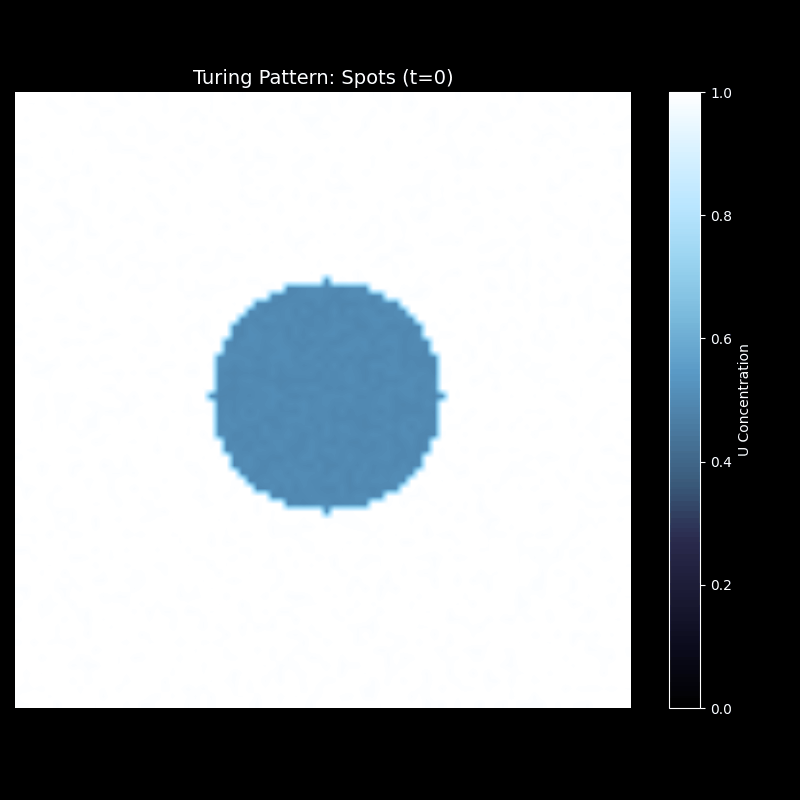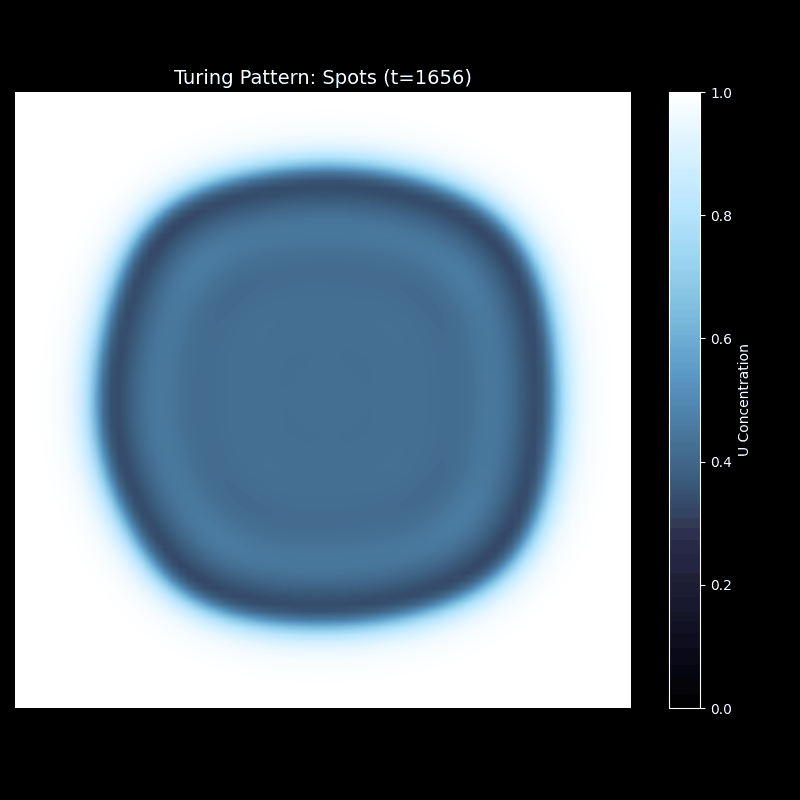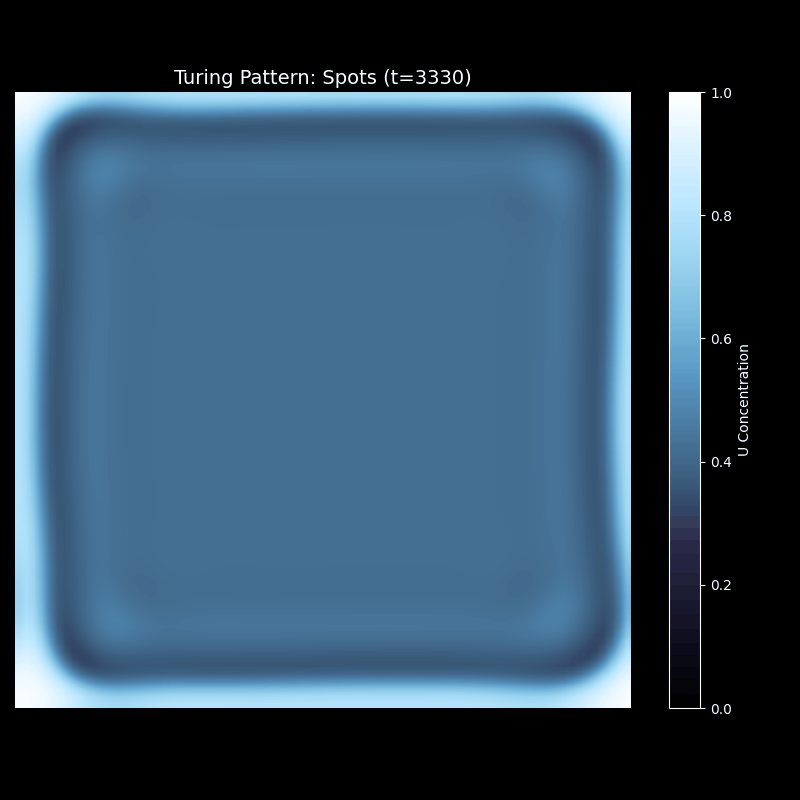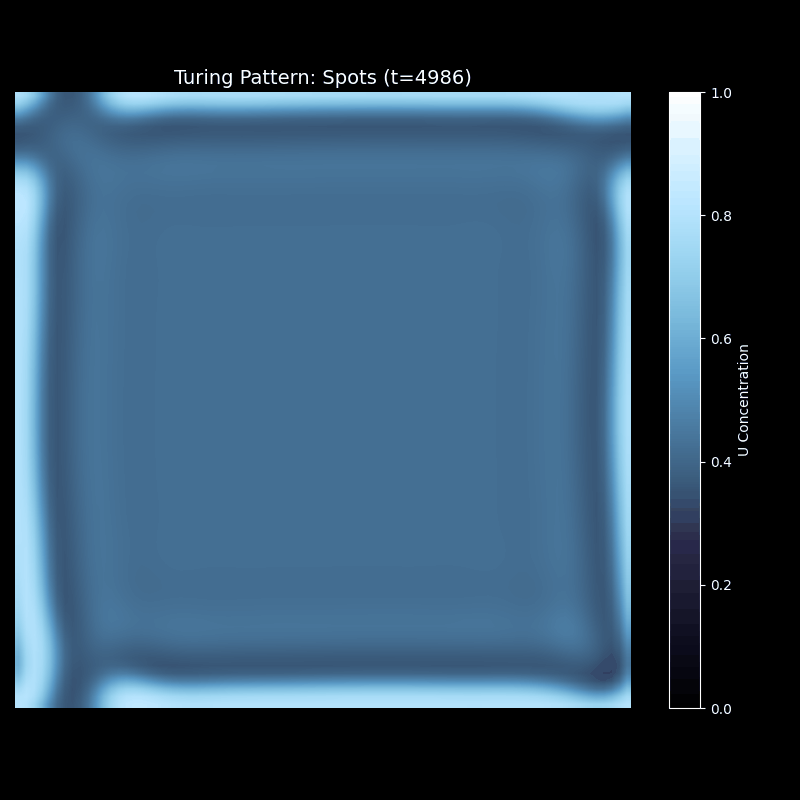
观察这个演化过程：最初，整个区域几乎是均匀的（U 的浓度接近 1）。中心的小扰动开始扩散，形成一个圆形的低浓度区域。随着时间推移，这个圆形区域开始分裂，边缘出现不稳定性，形成多个小的"芽"。这些芽继续生长、分裂，最终形成六边形排列的斑点图案——这种结构能最有效地平衡激活和抑制的作用范围。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.colors import LinearSegmentedColormap
# 参数设置
SIZE = 80
DU = 0.16
DV = 0.08
FEED = 0.062
KILL = 0.061
N_STEPS = 5000
MAX_FRAMES = 270
class TuringSimulator:
    """Gray-Scott反应扩散系统模拟器"""    
    def __init__(self, size, du, dv, feed, kill):
        self.size = size
        self.du = du
        self.dv = dv
        self.feed = feed
        self.kill = kill        
        # 初始化浓度场
        self.U = np.ones((size, size))
        self.V = np.zeros((size, size))        
        # 中心扰动
        r = 15
        center = size // 2
        y, x = np.ogrid[-center:size-center, -center:size-center]
        mask = x*x + y*y <= r*r
        self.U[mask] = 0.50
        self.V[mask] = 0.25        
        # 随机扰动
        self.U += np.random.uniform(-0.01, 0.01, (size, size))
        self.V += np.random.uniform(-0.01, 0.01, (size, size))
        self.U = np.clip(self.U, 0, 1)
        self.V = np.clip(self.V, 0, 1)        
    def laplacian(self, field):
        """计算拉普拉斯算子（周期边界）"""
        return (
            np.roll(field, 1, axis=0) +
            np.roll(field, -1, axis=0) +
            np.roll(field, 1, axis=1) +
            np.roll(field, -1, axis=1) -
            4 * field
        )    
    def step(self, dt=1.0):
        """执行一个时间步"""
        uvv = self.U * self.V * self.V        
        dU = self.du * self.laplacian(self.U) -Uvv + self.feed * (1 - self.U)
        dV = self.dv * self.laplacian(self.V) + uvv - (self.feed + self.kill) * self.V        
        self.U += dt * dU
        self.V += dt * dV
        self.U = np.clip(self.U, 0, 1)
        self.V = np.clip(self.V, 0, 1)
# 创建模拟器
print(f"模拟斑点图案 ({SIZE}x{SIZE}, {N_STEPS} 步)...")
sim = TuringSimulator(SIZE, DU, DV, FEED, KILL)
# 采样帧
step_per_frame = max(1, N_STEPS // MAX_FRAMES)
frames_data = [sim.U.copy()]
for i in range(N_STEPS):
    sim.step()
    if (i + 1) % step_per_frame == 0:
        frames_data.append(sim.U.copy())
    if (i + 1) % 1000 == 0:
        print(f"  {i+1}/{N_STEPS}")
print(f"完成! 共 {len(frames_data)} 帧")
# 黑底蓝白配色
colors = ['#000000', '#0a0a1a', '#1a1a33', '#2a2a4d', 
          '#3a5a7a', '#4a7aa0', '#5a9ac6', '#7abadc',
          '#9ad4f0', '#bae6ff', '#daf2ff', '#ffffff']
cmap = LinearSegmentedColormap.from_list('turing', colors, N=256)
# 可视化
plt.style.use('dark_background')
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_aspect('equal')
ax.axis('off')
im = ax.imshow(frames_data[0], cmap=cmap, vmin=0, vmax=1, 
               interpolation='bilinear', origin='lower')
title = ax.set_title('Turing Pattern: Spots', fontsize=14, color='white')
cbar = plt.colorbar(im, ax=ax, shrink=0.8)
cbar.set_label('U Concentration', color='white')
plt.tight_layout()
def update(frame):
    im.set_array(frames_data[frame])
    title.set_text(f'Turing Pattern: Spots (t={frame*step_per_frame})')
    return [im, title]
ani = FuncAnimation(fig, update, frames=len(frames_data), interval=50, blit=True)
ani.save('../images/07_turing_spots.gif', writer='pillow', fps=20)
print(f"\n动画已保存: {len(frames_data)} 帧 @ 20 fps")

上述代码的运行效果为

条纹图案

条纹的形成过程更加动态。初始扰动迅速扩展成波浪状的前沿，这些波浪相互干涉，形成明暗交替的带状结构。随着时间推移，条纹逐渐稳定，取向基本确定。最终的图案具有近似平行的条纹，但局部会有分叉、弯曲——正如真实斑马身上的条纹并非完美平行。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.colors import LinearSegmentedColormap
# 参数设置（条纹图案）
# Gray-Scott模型参数：条纹需要较低的feed和适中的kill
SIZE = 100
DU = 0.14
DV = 0.06
FEED = 0.026  # 低feed产生细长条纹
KILL = 0.052  # 适中kill保持V存活
N_STEPS = 8000
MAX_FRAMES = 270
class TuringSimulator:
    """Gray-Scott反应扩散系统模拟器"""    
    def __init__(self, size, du, dv, feed, kill):
        self.size = size
        self.du = du
        self.dv = dv
        self.feed = feed
        self.kill = kill        
        # 初始化浓度场
        self.U = np.ones((size, size))
        self.V = np.zeros((size, size))        
        # 多点随机扰动（条纹需要更分散的初始种子）
        np.random.seed(42)
        n_seeds = 20
        for _ in range(n_seeds):
            cx = np.random.randint(10, size-10)
            cy = np.random.randint(10, size-10)
            r = np.random.randint(3, 8)
            y, x = np.ogrid[:size, :size]
            mask = (x - cx)**2 + (y - cy)**2 <= r**2
            self.U[mask] = 0.50
            self.V[mask] = 0.25        
        # 轻微随机扰动
        self.U += np.random.uniform(-0.02, 0.02, (size, size))
        self.V += np.random.uniform(-0.02, 0.02, (size, size))
        self.U = np.clip(self.U, 0, 1)
        self.V = np.clip(self.V, 0, 1)        
    def laplacian(self, field):
        """计算拉普拉斯算子（周期边界）"""
        return (
            np.roll(field, 1, axis=0) +
            np.roll(field, -1, axis=0) +
            np.roll(field, 1, axis=1) +
            np.roll(field, -1, axis=1) -
            4 * field
        )    
    def step(self, dt=1.0):
        """执行一个时间步"""
        uvv = self.U * self.V * self.V        
        dU = self.du * self.laplacian(self.U) -Uvv + self.feed * (1 - self.U)
        dV = self.dv * self.laplacian(self.V) + uvv - (self.feed + self.kill) * self.V        
        self.U += dt * dU
        self.V += dt * dV
        self.U = np.clip(self.U, 0, 1)
        self.V = np.clip(self.V, 0, 1)
# 创建模拟器
print(f"模拟条纹图案 ({SIZE}x{SIZE}, {N_STEPS} 步)...")
sim = TuringSimulator(SIZE, DU, DV, FEED, KILL)
# 采样帧
step_per_frame = max(1, N_STEPS // MAX_FRAMES)
frames_data = [sim.U.copy()]
for i in range(N_STEPS):
    sim.step()
    if (i + 1) % step_per_frame == 0:
        frames_data.append(sim.U.copy())
    if (i + 1) % 1000 == 0:
        print(f"  {i+1}/{N_STEPS}")
print(f"完成! 共 {len(frames_data)} 帧")
# 黑底蓝白配色
colors = ['#000000', '#0a0a1a', '#1a1a33', '#2a2a4d', 
          '#3a5a7a', '#4a7aa0', '#5a9ac6', '#7abadc',
          '#9ad4f0', '#bae6ff', '#daf2ff', '#ffffff']
cmap = LinearSegmentedColormap.from_list('turing', colors, N=256)
# 可视化
plt.style.use('dark_background')
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_aspect('equal')
ax.axis('off')
im = ax.imshow(frames_data[0], cmap=cmap, vmin=0, vmax=1, 
               interpolation='bilinear', origin='lower')
title = ax.set_title('Turing Pattern: Stripes', fontsize=14, color='white')
cbar = plt.colorbar(im, ax=ax, shrink=0.8)
cbar.set_label('U Concentration', color='white')
plt.tight_layout()
def update(frame):
    im.set_array(frames_data[frame])
    title.set_text(f'Turing Pattern: Stripes (t={frame*step_per_frame})')
    return [im, title]
ani = FuncAnimation(fig, update, frames=len(frames_data), interval=50, blit=True)
ani.save('../images/07_turing_stripes.gif', writer='pillow', fps=20)
print(f"\n动画已保存: {len(frames_data)} 帧 @ 20 fps")

上述代码的运行效果为

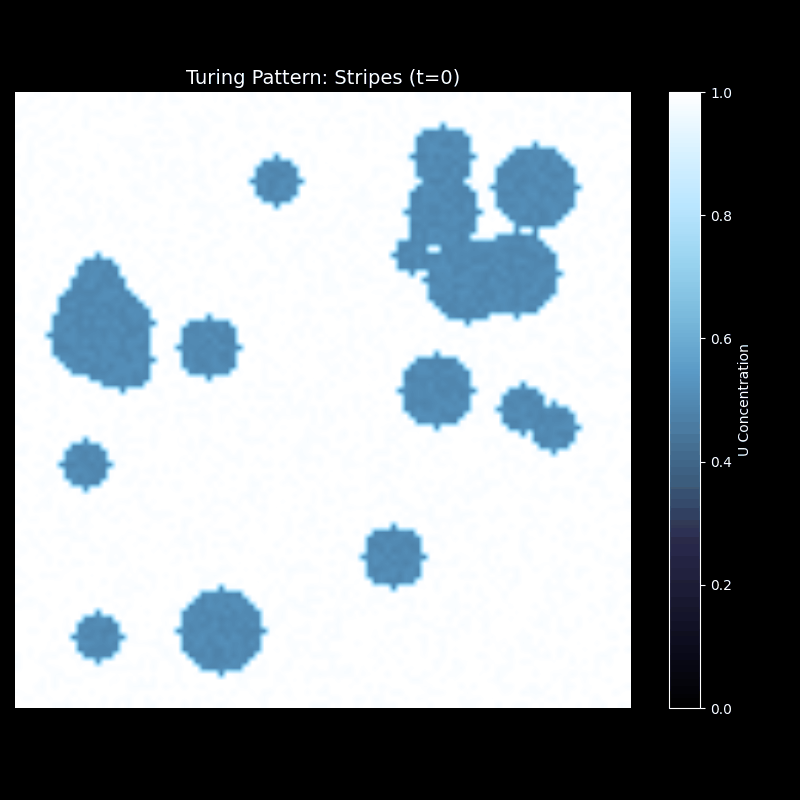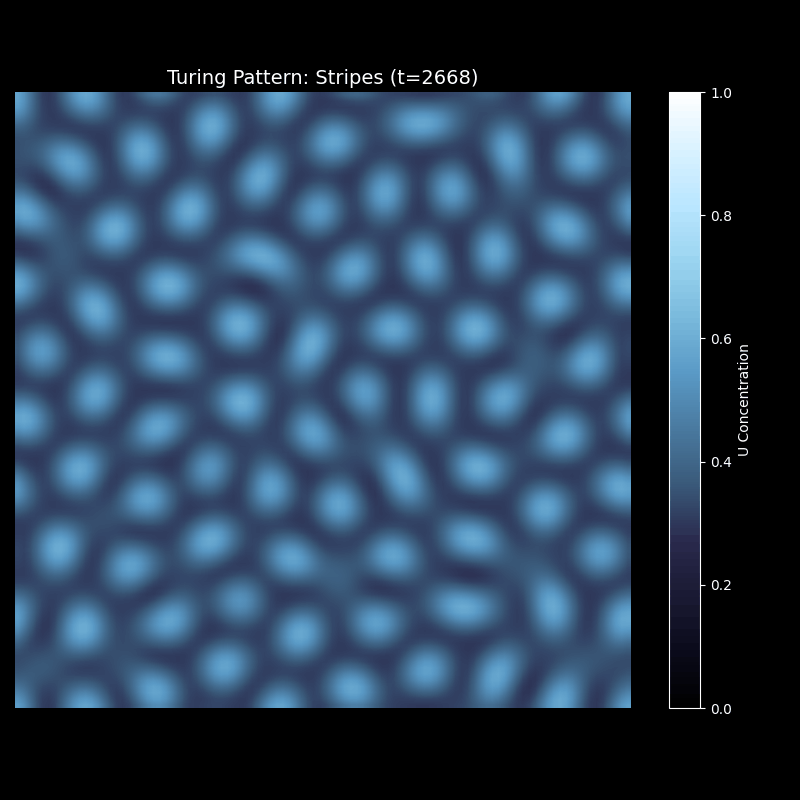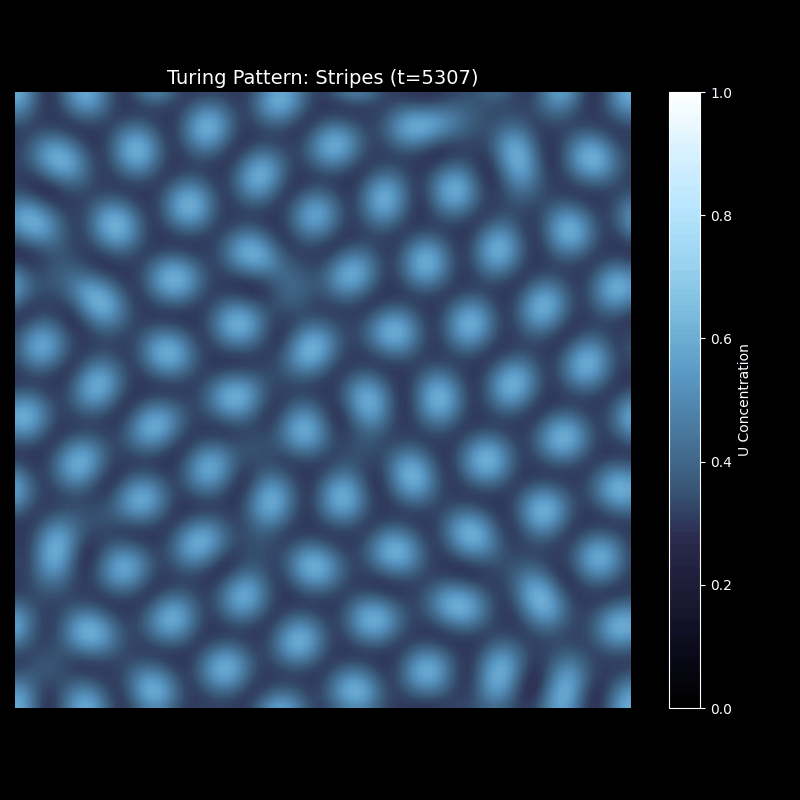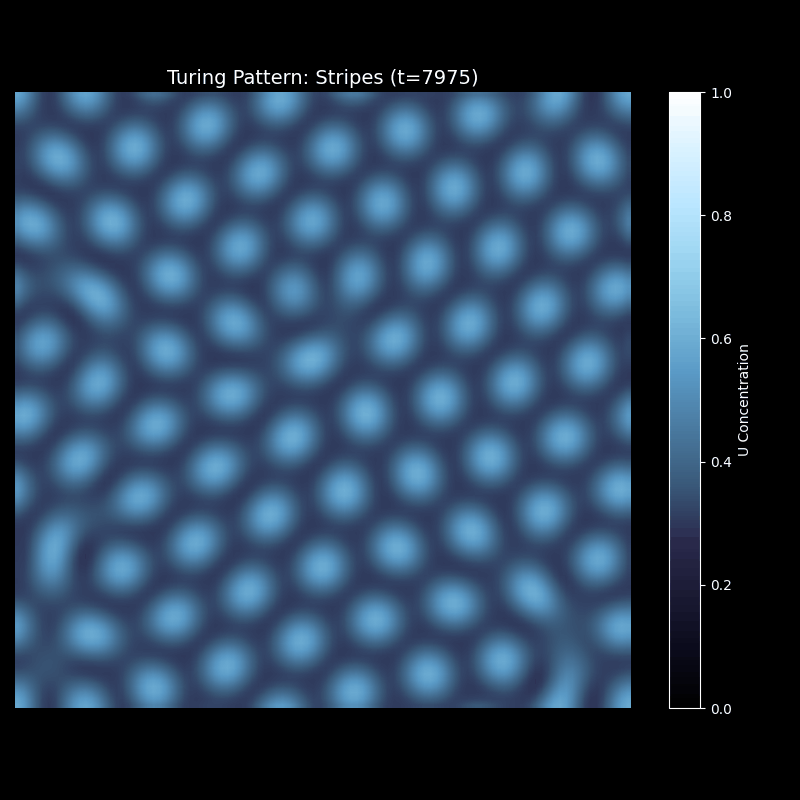
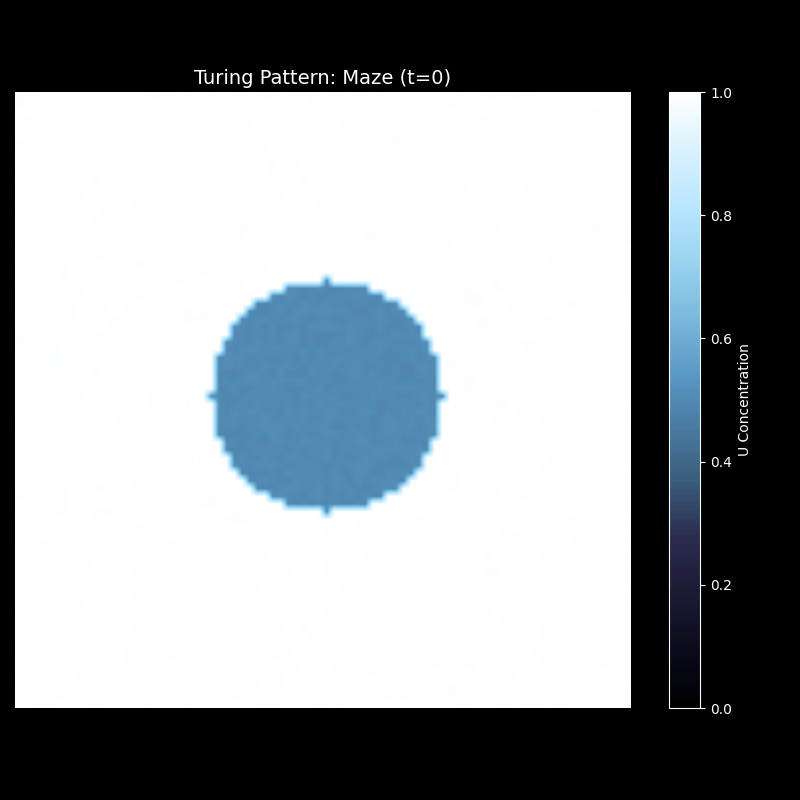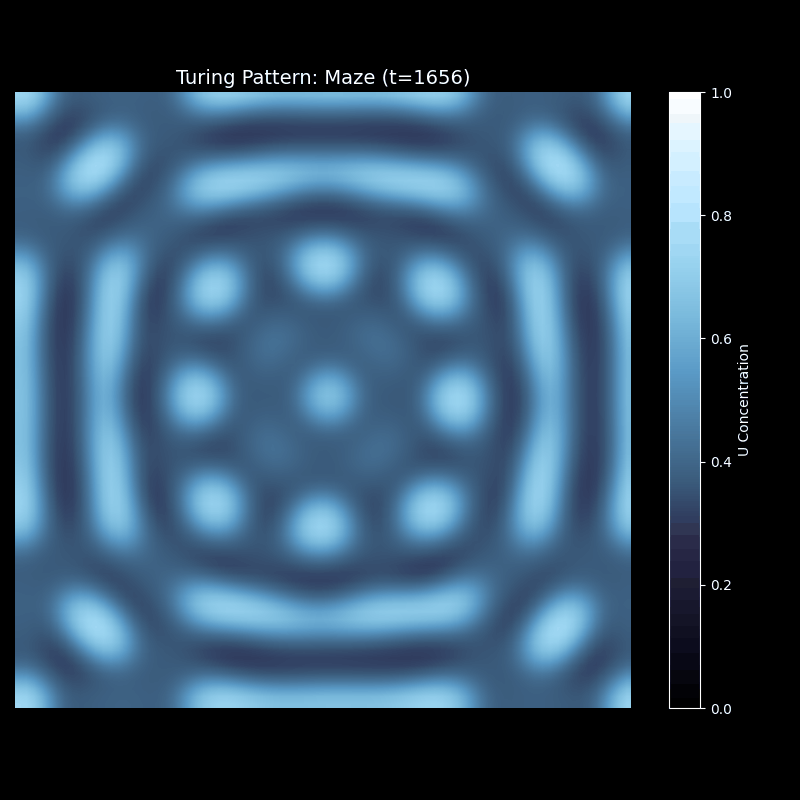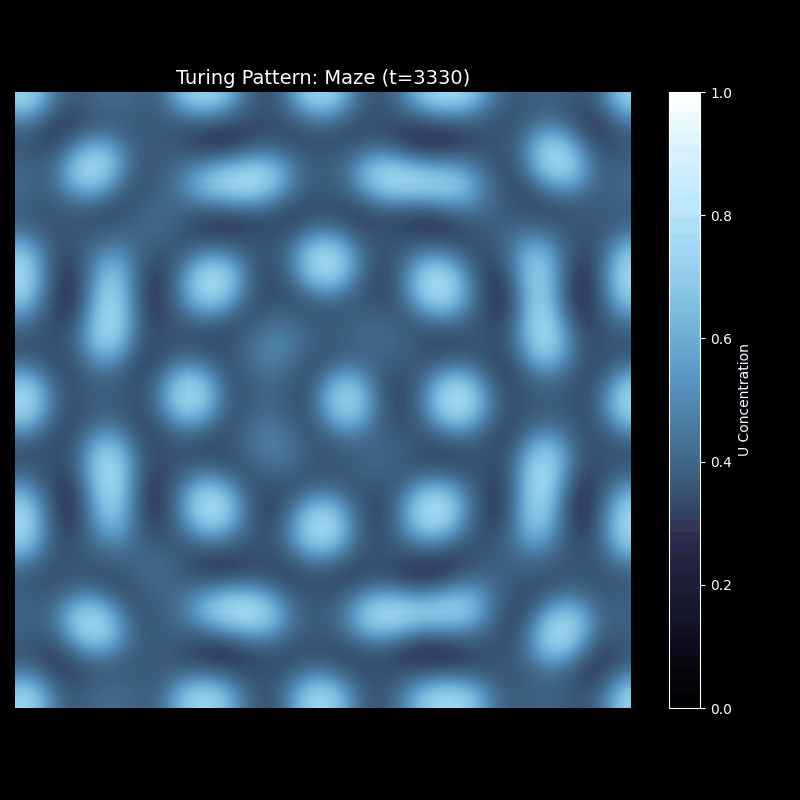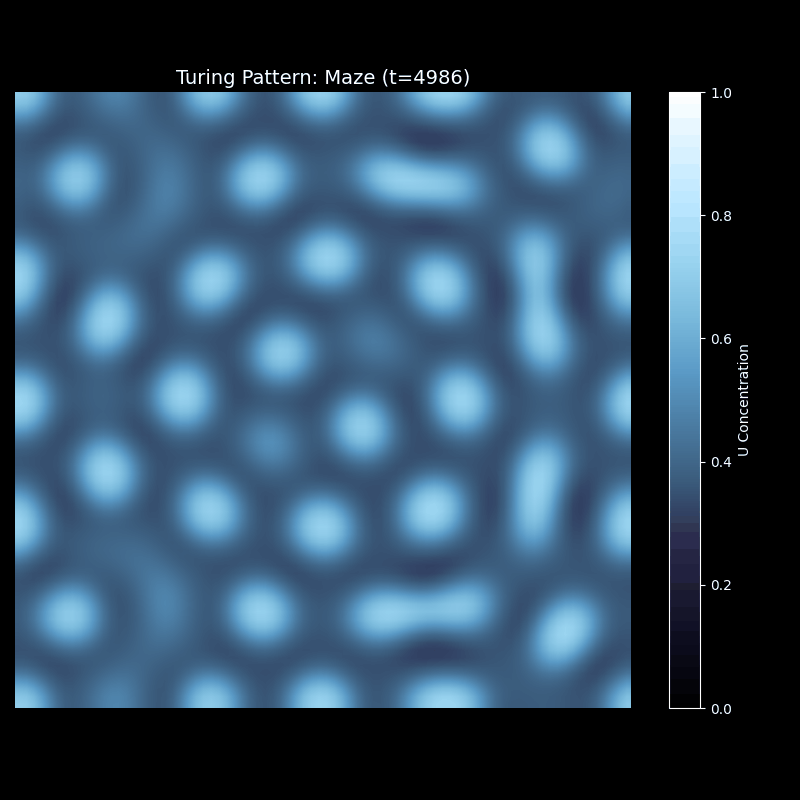
迷宫图案

迷宫图案的演化最为复杂。初期像条纹一样生长，但很快这些条纹开始连接、分支，形成网络状结构。有些通道会闭合成环，有些会分叉成树状。最终稳定的图案像一个复杂的迷宫，充满了曲折的通道。这种图案在自然界中也有对应——珊瑚的生长纹理、大脑皮层的沟回，都呈现类似的拓扑结构。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.colors import LinearSegmentedColormap
# 参数设置（迷宫图案）
SIZE = 80
DU = 0.16
DV = 0.08
FEED = 0.039
KILL = 0.058
N_STEPS = 5000
MAX_FRAMES = 270
class TuringSimulator:
    """Gray-Scott反应扩散系统模拟器"""    
    def __init__(self, size, du, dv, feed, kill):
        self.size = size
        self.du = du
        self.dv = dv
        self.feed = feed
        self.kill = kill        
        # 初始化浓度场
        self.U = np.ones((size, size))
        self.V = np.zeros((size, size))        
        # 中心扰动
        r = 15
        center = size // 2
        y, x = np.ogrid[-center:size-center, -center:size-center]
        mask = x*x + y*y <= r*r
        self.U[mask] = 0.50
        self.V[mask] = 0.25        
        # 随机扰动
        self.U += np.random.uniform(-0.01, 0.01, (size, size))
        self.V += np.random.uniform(-0.01, 0.01, (size, size))
        self.U = np.clip(self.U, 0, 1)
        self.V = np.clip(self.V, 0, 1)        
    def laplacian(self, field):
        """计算拉普拉斯算子（周期边界）"""
        return (
            np.roll(field, 1, axis=0) +
            np.roll(field, -1, axis=0) +
            np.roll(field, 1, axis=1) +
            np.roll(field, -1, axis=1) -
            4 * field
        )    
    def step(self, dt=1.0):
        """执行一个时间步"""
        uvv = self.U * self.V * self.V        
        dU = self.du * self.laplacian(self.U) -Uvv + self.feed * (1 - self.U)
        dV = self.dv * self.laplacian(self.V) + uvv - (self.feed + self.kill) * self.V        
        self.U += dt * dU
        self.V += dt * dV
        self.U = np.clip(self.U, 0, 1)
        self.V = np.clip(self.V, 0, 1)
# 创建模拟器
print(f"模拟迷宫图案 ({SIZE}x{SIZE}, {N_STEPS} 步)...")
sim = TuringSimulator(SIZE, DU, DV, FEED, KILL)
# 采样帧
step_per_frame = max(1, N_STEPS // MAX_FRAMES)
frames_data = [sim.U.copy()]
for i in range(N_STEPS):
    sim.step()
    if (i + 1) % step_per_frame == 0:
        frames_data.append(sim.U.copy())
    if (i + 1) % 1000 == 0:
        print(f"  {i+1}/{N_STEPS}")
print(f"完成! 共 {len(frames_data)} 帧")
# 黑底蓝白配色
colors = ['#000000', '#0a0a1a', '#1a1a33', '#2a2a4d', 
          '#3a5a7a', '#4a7aa0', '#5a9ac6', '#7abadc',
          '#9ad4f0', '#bae6ff', '#daf2ff', '#ffffff']
cmap = LinearSegmentedColormap.from_list('turing', colors, N=256)
# 可视化
plt.style.use('dark_background')
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_aspect('equal')
ax.axis('off')
im = ax.imshow(frames_data[0], cmap=cmap, vmin=0, vmax=1, 
               interpolation='bilinear', origin='lower')
title = ax.set_title('Turing Pattern: Maze', fontsize=14, color='white')
cbar = plt.colorbar(im, ax=ax, shrink=0.8)
cbar.set_label('U Concentration', color='white')
plt.tight_layout()
def update(frame):
    im.set_array(frames_data[frame])
    title.set_text(f'Turing Pattern: Maze (t={frame*step_per_frame})')
    return [im, title]
ani = FuncAnimation(fig, update, frames=len(frames_data), interval=50, blit=True)
ani.save('../images/07_turing_maze.gif', writer='pillow', fps=20)
print(f"\n动画已保存: {len(frames_data)} 帧 @ 20 fps")

上述代码的运行效果为

生物学意义

图灵的理论在发表后的几十年内，一直被视为纯粹的数学推测。直到后来，科学家才在真实生物中找到确凿的证据，验证了图灵模型的预测：图案的形态由化学物质的扩散和反应速率决定，而非由基因直接"编码"每个毛囊的位置。

斑马的条纹、豹子的斑点、热带鱼的花纹——都可能起源于类似的反应扩散机制；植物的叶序排列（如向日葵种子的螺旋）、沙丘的波纹、云层的卷积，甚至社会学中的聚居模式，都可以用图灵型方程来描述。

数学视角

图灵的原始论文使用了线性稳定性分析来预测哪些参数组合会产生图案。基本思路是：假设系统从均匀状态开始，加入一个微小的空间扰动（如正弦波）。如果这个扰动随时间增长，系统就不稳定，会自发形成图案；如果衰减，系统保持均匀。

线性稳定性分析

考虑一般的双组分反应扩散系统，在均匀平衡点 $(u_0, v_0)$ 附近进行线性化。设小扰动为：

$$u = u_0 + \delta u, \quad v = v_0 + \delta v$$

将扰动分解为傅里叶模式：

$$\delta u = \sum_k \hat{u}_k e^{i\mathbf{k}\cdot\mathbf{x} + \lambda_k t}$$

$$\delta v = \sum_k \hat{v}_k e^{i\mathbf{k}\cdot\mathbf{x} + \lambda_k t}$$

其中 $\mathbf{k}$ 是波矢，$|\mathbf{k}| = 2\pi/\lambda$ 是波数，$\lambda_k$ 是增长率。代入线性化方程，得到特征值问题：

$$\lambda_k = \frac{\tau_k \pm \sqrt{\tau_k^2 - 4\Delta_k}}{2}$$

其中迹和行列式为：

$$\tau_k = f_u + g_v - (D_u + D_v)k^2$$

$$\Delta_k = (f_u - D_u k^2)(g_v - D_v k^2) - f_v g_u$$

这里 $f_u = \frac{\partial f}{\partial u}\big|_{(u_0,v_0)}$ 等是边际反应速率（雅可比矩阵元素）。

图灵不稳定性条件

图灵不稳定性要求[2]： 1. 无扩散时稳定：$f_u + g_v < 0$ 且 $f_u g_v - f_v g_u > 0$ 2. 有扩散时不稳定：存在某些波数 $k$ 使得 $\text{Re}(\lambda_k) > 0$ 3. 扩散系数差异：$D_v > D_u$（关键条件！）

关键发现是：某些波长的扰动会增长，某些会衰减。增长最快的那个波长，就是最终图案的特征尺寸。这解释了为什么斑点有特定的间距、条纹有特定的宽度——它们不是任意的，而是由系统的物理参数（扩散系数、反应速率）唯一确定的。

化学波长由下式给出：

$$\lambda_c = 2\pi \sqrt{\frac{D_u D_v}{(d\sqrt{D_u/D_v} - a\sqrt{D_v/D_u})^2/4 - bc}}$$

这个波长对应增长率 $\lambda_k$ 的最大值点。

总结

图灵的形态发生理论展示了数学建模的最高境界：用简洁的方程捕捉复杂现象的本质。两个偏微分方程、四个参数，就能重现从斑点到条纹、从迷宫到螺旋的各种自然图案。这不仅是数学的胜利，更揭示了自然界深层的统一性——看似千差万别的形态，可能遵循相同的生成规律。

这个模型也提醒我们：复杂性不等于复杂的规则。简单的局部相互作用，通过空间和时间的累积，可以涌现出令人惊叹的全局秩序。这个思想贯穿了现代科学的多个领域——从凝聚态物理到神经科学，从生态学到经济学，都在探索"简单规则如何产生复杂系统"。

图灵在 1952 年就预见了这一切，而我们今天依然在他开辟的道路上前行。

可参考的文献

[1] Turing, A. M. (1952). The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 237(641), 37-72. https://doi.org/10.1098/rstb.1952.0012

[2] Murray, J. D. (2003). Mathematical Biology II: Spatial Models and Biomedical Applications (3rd ed.). Springer. https://doi.org/10.1007/b98868

[3] Sick, S., Reinker, S., Timmer, J., & Schlake, T. (2006). WNT and DKK determine hair follicle spacing through a reaction-diffusion mechanism. Science, 314(5804), 1447-1450. https://doi.org/10.1126/science.1130088

[4] Pearson, J. E. (1993). Complex patterns in a simple system. Science, 261(5118), 189-192. https://doi.org/10.1126/science.261.5118.189

[5] Gray, P., & Scott, S. K. (1985). Sustained oscillations and other exotic patterns of behavior in isothermal reactions. Journal of Physical Chemistry, 89(1), 22-32. https://doi.org/10.1021/j100247a009